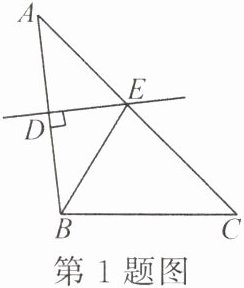
1. 如图,在$\triangle ABC$中,$AC = 8$,$BC = 5$,$AB$的垂直平分线$DE$交$AB$于点$D$,交$AC$于点$E$,则$\triangle BCE$的周长为(
A.13
B.17
C.18
D.21
A
)
A.13
B.17
C.18
D.21
答案:
1.A
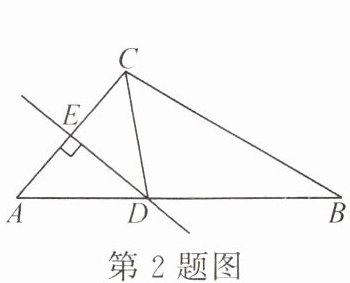
2. 如图,在$\triangle ABC$中,$AC$的垂直平分线交$AB$于点$D$,垂足为点$E$,$CD$平分$\angle ACB$,若$\angle A = 50^{\circ}$,则$\angle B$的度数为(
A.$25^{\circ}$
B.$30^{\circ}$
C.$35^{\circ}$
D.$40^{\circ}$
B
)
A.$25^{\circ}$
B.$30^{\circ}$
C.$35^{\circ}$
D.$40^{\circ}$
答案:
2.B
3. 如图,在$\triangle ABC$中,$\angle BAC = 110^{\circ}$,$AB$的垂直平分线交$BC$于点$D$,$AC$的垂直平分线交$BC$于点$E$,则$\angle DAE$的度数为

40°
。
答案:
3.40°
4. 尺规作图:如图,有三家公司$A$,$B$,$C$,现要建一个健身中心,且健身中心到三家公司的距离相等,请找出健身中心$P$的位置。
 ]
]
 ]
]
答案:
4.解:如图,分别作线段AB,BC的垂直平分线,相交于点P,则点P即为所求.

4.解:如图,分别作线段AB,BC的垂直平分线,相交于点P,则点P即为所求.

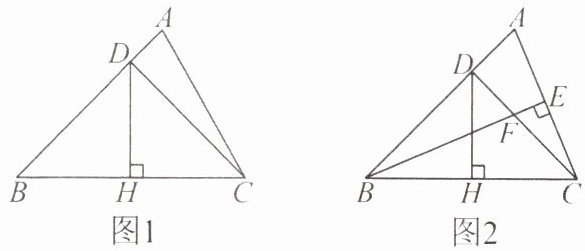
5. 已知,如图 1,$D$是$\triangle ABC$中$AB$上一点,并且$\angle BDC = 90^{\circ}$,$DH$垂直平分$BC$交$BC$于点$H$。
(1)请说明$DB = DC$的依据。
(2)如图 2,若$BE \perp AC$于点$E$,与$CD$相交于点$F$,求证:$\triangle BDF \cong \triangle CDA$。
]
(1)请说明$DB = DC$的依据。
(2)如图 2,若$BE \perp AC$于点$E$,与$CD$相交于点$F$,求证:$\triangle BDF \cong \triangle CDA$。
]

答案:
5.
(1)解:依据是线段垂直平分线上的点到线段两端点的距离相等.
(2)证明:
∵BE⊥AC,
∴∠BEC=90°=∠BDF.
∵∠BFD=∠CFE,
∴∠DBF=∠DCA.
在△BDF和△CDA中,
∵$\begin{cases} ∠BDF = ∠CDA,\\BD = CD,\\∠DBF = ∠DCA,\end{cases}$
∴△BDF≌△CDA(ASA).
(1)解:依据是线段垂直平分线上的点到线段两端点的距离相等.
(2)证明:
∵BE⊥AC,
∴∠BEC=90°=∠BDF.
∵∠BFD=∠CFE,
∴∠DBF=∠DCA.
在△BDF和△CDA中,
∵$\begin{cases} ∠BDF = ∠CDA,\\BD = CD,\\∠DBF = ∠DCA,\end{cases}$
∴△BDF≌△CDA(ASA).
查看更多完整答案,请扫码查看


