《2025年名师面对面学科素养评价八年级数学上册浙教版》

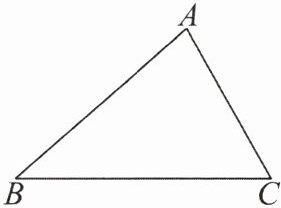
7. 如图，在$\triangle ABC$中，$\angle ABC = 40^{\circ}$，$\angle BAC = 80^{\circ}$。以点 $A$ 为圆心，$AC$长为半径作弧，交射线 $BA$ 于点 $D$，连结 $CD$，则$\angle BCD$的度数是10°或100°。

答案： 7.10°或100°

8. 如图，$BE$ 是$\triangle ABC$的角平分线，在 $AB$ 上取点 $D$，使 $DB = DE$。
（1）求证：$DE // BC$。
（2）若$\angle A = 65^{\circ}$，$\angle AED = 45^{\circ}$，求$\angle EBC$的度数。

答案： 8.
(1)证明：
∵BE是△ABC的角平分线，
∴∠DBE=∠EBC.
∵DB=DE，
∴∠DEB=∠DBE，
∴∠DEB=∠EBC，
∴DE//BC；
(2)解：
∵DE//BC，
∴∠C=∠AED=45°，
∴∠ABC=180°-∠A-∠C=70°.
∵BE是△ABC的角平分线，
∴∠EBC=$\frac{1}{2}$∠ABC=35°.

9. 如图，$P$，$Q$ 分别是等边三角形 $ABC$ 边 $AB$，$BC$ 上的动点（端点除外），点 $P$，$Q$ 以相同的速度同时从点 $A$，$B$ 出发。
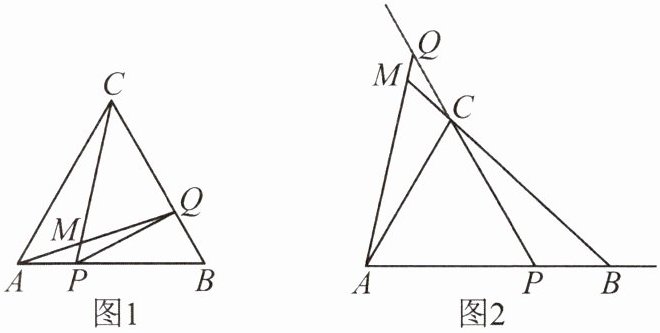
（1）如图 1，连结 $AQ$，$CP$。求证：$\triangle ABQ \cong \triangle CAP$。
（2）如图 1，当点 $P$，$Q$ 分别在边 $AB$，$BC$ 上运动时，$AQ$，$CP$ 相交于点 $M$，$\angle QMC$的大小是否变化？若变化，请说明理由；若不变，求出它的度数。
（3）如图 2，当点 $P$，$Q$ 分别在 $AB$，$BC$ 的延长线上运动时，直线 $AQ$，$CP$ 相交于点 $M$，$\angle QMC$的大小是否变化？若变化，请说明理由；若不变，求出它的度数。

答案： 9.
(1)证明：
∵△ABC是等边三角形，
∴∠ABQ=∠CAP=60°，AB=CA.
又
∵点P，Q运动速度相同，
∴AP=BQ.
∴△ABQ≌△CAP(SAS)；
(2)解：当点P，Q分别在边AB，BC上运动时，∠QMC的大小不变.
∵△ABQ≌△CAP，
∴∠BAQ=∠ACP.
∵∠QMC是△ACM的外角，
∴∠QMC=∠ACP+∠MAC=∠BAQ+∠MAC=∠BAC=60°；
(3)解：当点P，Q分别在AB，BC的延长线上运动时，∠QMC的大小不变.
同理可得△ABQ≌△CAP，
∴∠BAQ=∠ACP.
∵∠QMC是△APM的外角，
∴∠QMC=∠BAQ+∠APM.
∴∠QMC=∠ACP+∠APM=180°-∠PAC=180°-60°=120°.
∴当点P，Q分别在AB，BC的延长线上运动时，∠QMC的度数为120°.