《2025年名师面对面学科素养评价八年级数学上册浙教版》

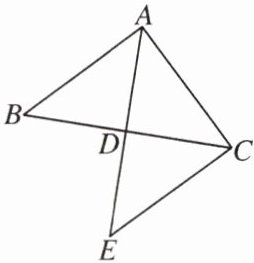
1. 如图，在$\triangle ABC$中，$D$是边$BC$的中点，连结$AD$并延长到点$E$，使$DE = AD$，连结$CE$。
(1) 求证：$\triangle ABD\cong\triangle ECD$。
(2) 若$\triangle ABD$的面积为$5$，求$\triangle ACE$的面积。

答案： 1.
(1)证明：
∵ D 是边 BC 的中点，
∴ BD = CD.
在△ABD 和△ECD 中，
$\begin{cases} BD = CD, \\ \angle ADB = \angle EDC, \\ AD = ED, \end{cases}$
∴ △ABD≌△ECD(SAS);
(2)解：在△ABC 中，
∵ D 是边 BC 的中点，
∴ $S_{\triangle ABD} = S_{\triangle ADC}$.由
(1)知△ABD≌△ECD，
∴ $S_{\triangle ABD} = S_{\triangle ECD}$.
∵ $S_{\triangle ABD} = 5$，
∴ $S_{\triangle ACE} = S_{\triangle ADC} + S_{\triangle ECD} = 5 + 5 = 10$.

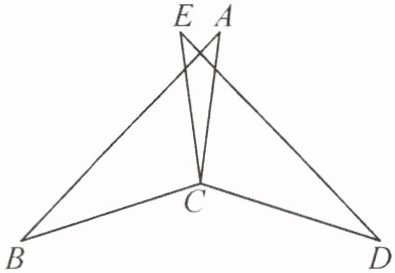
2. 如图，已知$EC = AC$，$\angle BCE = \angle DCA$，$\angle A = \angle E$，求证：$BC = DC$。

答案： 2.证明：
∵ ∠BCE = ∠DCA，
∴ ∠BCE + ∠ACE = ∠DCA + ∠ACE，
即 ∠ACB = ∠ECD.
在△ABC 和△EDC 中，
$\begin{cases} \angle ACB = \angle ECD, \\ AC = EC, \\ \angle A = \angle E, \end{cases}$
∴ △ABC≌△EDC(ASA)，
∴ BC = DC.