1. 如图,下列推理不正确的是(
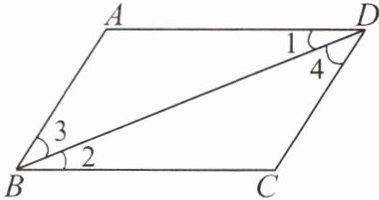
A.∵AB//CD,∴∠ABC + ∠C = 180°
B.∵∠1 = ∠2,∴AD//BC
C.∵AD//BC,∴∠3 = ∠4
D.∵∠A + ∠ADC = 180°,∴AB//CD
C
)
A.∵AB//CD,∴∠ABC + ∠C = 180°
B.∵∠1 = ∠2,∴AD//BC
C.∵AD//BC,∴∠3 = ∠4
D.∵∠A + ∠ADC = 180°,∴AB//CD
答案:
1.C
2. 如图,把一块三角板ABC的直角顶点B放在直线EF上,∠C = 30°,AC//EF,则∠1 =(
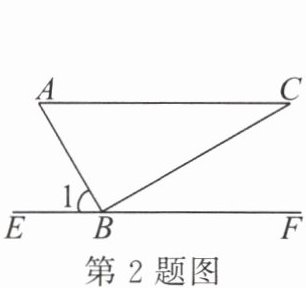
A.30°
B.45°
C.60°
D.75°
C
)
A.30°
B.45°
C.60°
D.75°
答案:
2.C
3. 如图,请填写一个条件,使结论成立:因为

∠1=∠4
,所以a//b.
答案:
3.∠1=∠4(答案不唯一)
4. 如图,AD⊥BC于点D,EG⊥BC于点G,∠E = ∠1. 求证:AD平分∠BAC.
证明:(请在括号里填写理由)
∵AD⊥BC于点D,EG⊥BC于点G(
∴∠ADC = ∠EGC = 90°(
∴AD//EG(
∴∠1 = ∠2(
∠E = ∠3(
又∵∠E = ∠1(
∴∠2 = ∠3(
∴AD平分∠BAC(
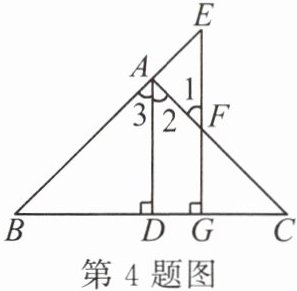
证明:(请在括号里填写理由)
∵AD⊥BC于点D,EG⊥BC于点G(
已知
),∴∠ADC = ∠EGC = 90°(
垂直的定义
),∴AD//EG(
同位角相等,两直线平行
),∴∠1 = ∠2(
两直线平行,内错角相等
),∠E = ∠3(
两直线平行,同位角相等
).又∵∠E = ∠1(
已知
),∴∠2 = ∠3(
等量代换
),∴AD平分∠BAC(
角平分线的定义
).
答案:
4.已知 垂直的定义 同位角相等,两直线平行 两直线平行,内错角相等 两直线平行,同位角相等 已知 等量代换 角平分线的定义
5. 如图,AB//DE,∠1 = ∠2. 试判断AE与DC的位置关系,并说明理由.
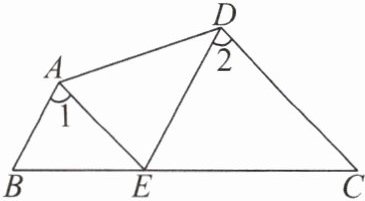

答案:
5.解:AE//DC.理由如下:
∵AB//DE(已知),
∴∠1=∠AED(两直线平行,内错角相等).
∵∠1=∠2(已知),
∴∠AED=∠2(等量代换),
∴AE//DC(内错角相等,两直线平行).
∵AB//DE(已知),
∴∠1=∠AED(两直线平行,内错角相等).
∵∠1=∠2(已知),
∴∠AED=∠2(等量代换),
∴AE//DC(内错角相等,两直线平行).
查看更多完整答案,请扫码查看


