《2025年名师面对面学科素养评价八年级数学上册浙教版》

1. 下列条件中，能判定$\triangle ABC$为等腰三角形的是(C)

A.$\angle A = 30^{\circ}$，$\angle B = 60^{\circ}$
B.$AB = AC = 2$，$BC = 4$
C.$\angle A = 50^{\circ}$，$\angle B = 80^{\circ}$
D.$AB = 3$，$BC = 7$，周长为$13$

答案： 1.C

2. 如图，在$\triangle ABC$中，$AD\perp BC$于点$D$，下列条件中，不能判定$\triangle ABC$为等腰三角形的是(A)

A.$\angle BAC = 60^{\circ}$
B.$\angle B = \angle C$
C.$AB = AC$
D.$BD = CD$

答案： 2.A

3. 等腰三角形补充下列条件后，仍不一定成为等边三角形的是(C)

A.有一个内角是$60^{\circ}$
B.有一个外角是$120^{\circ}$
C.有两个角相等
D.腰与底边相等

答案： 3.C

4. 如图，在$\triangle ABC$中，$\angle A = 36^{\circ}$，$AB = AC$，$BD$平分$\angle ABC$。若$\triangle ABD$的周长比$\triangle BCD$的周长多$1\mathrm{cm}$，则$BD$的长是(B)

A.$0.5\mathrm{cm}$
B.$1\mathrm{cm}$
C.$1.5\mathrm{cm}$
D.$2\mathrm{cm}$

答案： 4.B

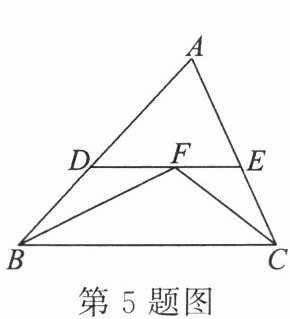
5. 如图，在$\triangle ABC$中，$BF$，$CF$分别平分$\angle ABC$和$\angle ACB$，过点$F$作$DE// BC$交$AB$于点$D$，交$AC$于点$E$。那么下列结论：①$\triangle BDF$和$\triangle CEF$都是等腰三角形；②$\angle DFB = \angle EFC$；③$\triangle ADE$的周长等于$AB$与$AC$的和；④$BF = CF$。其中正确的是①③。(填序号)

答案： 5.①③

6. 如图，在$\triangle ABC$中，$AD$平分$\angle BAC$，$EG// AD$。找出图中的等腰三角形，并给出证明。

]

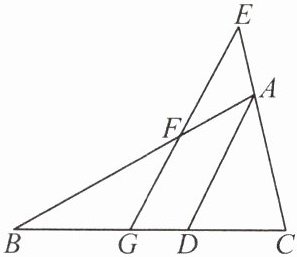
答案： 6.解:△AEF是等腰三角形.
　证明:
∵AD平分∠BAC，
∴∠BAD=∠CAD.
　又
∵EG//AD,
∴∠E=∠CAD,∠EFA=∠BAD,
∴∠E=∠EFA,
∴AE=AF,
∴△AEF是等腰三角形.