1. 如图,要用“HL”判定 $Rt\triangle ABC$ 和 $Rt\triangle DEF$ 全等的条件是(

A.$AC = DF$,$BC = EF$
B.$\angle A=\angle D$,$AB = DE$
C.$AC = DF$,$AB = DE$
D.$\angle B=\angle E$,$BC = EF$
C
)
A.$AC = DF$,$BC = EF$
B.$\angle A=\angle D$,$AB = DE$
C.$AC = DF$,$AB = DE$
D.$\angle B=\angle E$,$BC = EF$
答案:
1.C
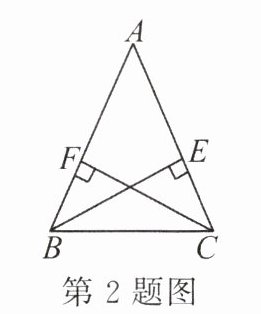
2. 如图所示,$BE\perp AC$,$CF\perp AB$,垂足分别是 $E$,$F$。若 $BE = CF$,则图中全等三角形有(
A.1 对
B.2 对
C.3 对
D.4 对
C
)
A.1 对
B.2 对
C.3 对
D.4 对
答案:
2.C
3. 如图,已知 $AB = DC$,下列条件中,不能使 $\triangle ABC\cong\triangle DCB$ 的是(

A.$AC = DB$
B.$\angle A=\angle D = 90^{\circ}$
C.$\angle ABC=\angle DCB$
D.$\angle ACB=\angle DBC$
D
)
A.$AC = DB$
B.$\angle A=\angle D = 90^{\circ}$
C.$\angle ABC=\angle DCB$
D.$\angle ACB=\angle DBC$
答案:
3.D
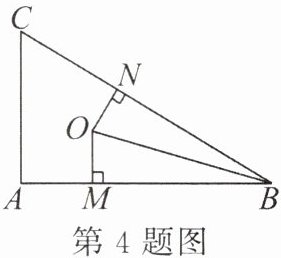
4. 如图所示,点 $O$ 在一块直角三角板 $ABC$ 上(其中 $\angle ABC = 30^{\circ}$),$OM\perp AB$ 于点 $M$,$ON\perp BC$ 于点 $N$。若 $OM = ON$,则 $\angle ABO=$
15°
。
答案:
4.15°
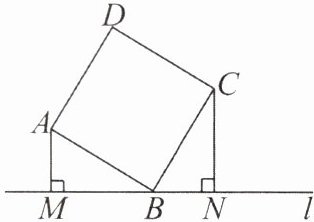
5. 如图,直线 $l$ 过正方形 $ABCD$ 的顶点 $B$,点 $A$,$C$ 到直线 $l$ 的距离分别是 1 和 2,则正方形的边长是
$\sqrt{5}$
。
答案:
5.$\sqrt{5}$
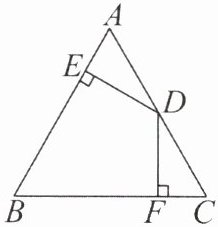
6. 如图,在 $\triangle ABC$ 中,$AB = AC$,$D$ 为 $AC$ 的中点,$DE\perp AB$,$DF\perp BC$,垂足分别为 $E$,$F$,且 $DE = DF$。求证:$\triangle ABC$ 是等边三角形。

答案:
6.证明:
∵AB=AC,
∴∠B=∠C.
∵DE⊥AB,DF⊥BC,
∴∠DEA=∠DFC=90°.
∵D为AC的中点,
∴DA=DC.
又
∵DE=DF,
∴Rt△ADE≌Rt△CDF(HL),
∴∠A=∠C,
∴∠A=∠B=∠C,
∴△ABC是等边三角形.
∵AB=AC,
∴∠B=∠C.
∵DE⊥AB,DF⊥BC,
∴∠DEA=∠DFC=90°.
∵D为AC的中点,
∴DA=DC.
又
∵DE=DF,
∴Rt△ADE≌Rt△CDF(HL),
∴∠A=∠C,
∴∠A=∠B=∠C,
∴△ABC是等边三角形.
查看更多完整答案,请扫码查看


