《2025年名师面对面学科素养评价八年级数学上册浙教版》

1. 下图中全等的三角形有(D)


A.Ⅰ和Ⅱ
B.Ⅱ和Ⅳ
C.Ⅱ和Ⅲ
D.Ⅰ和Ⅲ

答案： 1.D

2. 如图，已知 $ AB = AD $，$ AC = AE $。若要判定 $ \triangle ABC \cong \triangle ADE $，则下列添加的条件中，正确的是(C)

A.$ \angle 1 = \angle DAC $
B.$ \angle B = \angle D $
C.$ \angle 1 = \angle 2 $
D.$ \angle C = \angle E $

答案： 2.C

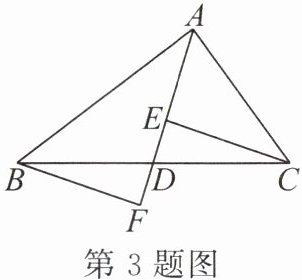
3. 如图，$ AD $ 是 $ \triangle ABC $ 的中线，$ E $，$ F $ 分别是 $ AD $ 和 $ AD $ 延长线上的点，且 $ DE = DF $，连结 $ BF $，$ CE $。有下列说法：① $ CE = BF $；② $ \triangle ABD $ 和 $ \triangle ACD $ 面积相等；③ $ BF // CE $；④ $ \triangle BDF \cong \triangle CDE $。其中正确的有(D)

A.1 个
B.2 个
C.3 个
D.4 个

答案： 3.D

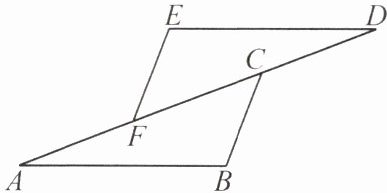
4. 如图，$ AB // DE $，$ AB = DE $，$ AF = DC $。求证：$ \angle B = \angle E $。

答案： 4.证明：
∵AB//DE,
∴∠A=∠D，
又
∵AF=DC,
∴AC=DF.
在△ABC和△DEF中，
∵$\begin{cases}AC=DF,\\∠A=∠D,\\AB=DE,\end{cases}$
∴△ABC≌△DEF(SAS),
∴∠B=∠E.

5. 如图，点 $ D $ 在 $ AB $ 上，点 $ E $ 在 $ AC $ 上，$ AB = AC $，$ AD = AE $。求证：$ BE = CD $。

答案： 5.证明：在△ADC和△AEB中，
∵$\begin{cases}AD=AE,\\∠A=∠A,\\AC=AB,\end{cases}$
∴△ADC≌△AEB(SAS),
∴BE=CD.