1. 已知△ABC 中,∠A,∠B,∠C 对应的三边分别是 a,b,c。若∠B = 90°,则有关系式(
A.$a^{2}+b^{2}=c^{2}$
B.$a^{2}+c^{2}=b^{2}$
C.$a^{2}-b^{2}=c^{2}$
D.$b^{2}+c^{2}=a^{2}$
B
)A.$a^{2}+b^{2}=c^{2}$
B.$a^{2}+c^{2}=b^{2}$
C.$a^{2}-b^{2}=c^{2}$
D.$b^{2}+c^{2}=a^{2}$
答案:
1.B
2. 已知等腰三角形的一条腰长是 5,底边长是 6,则它底边上的高为(
A.$\sqrt{11}$
B.3
C.4
D.5
C
)A.$\sqrt{11}$
B.3
C.4
D.5
答案:
2.C
3. 如图,有两棵树,一棵高 10 米,另一棵高 4 米,两树相距 8 米。一只小鸟从一棵树的树梢飞到另一棵树的树梢,则小鸟至少要飞行(
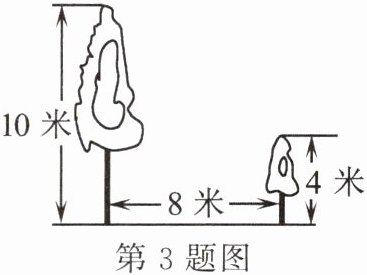
A.8 米
B.10 米
C.12 米
D.14 米
B
)
A.8 米
B.10 米
C.12 米
D.14 米
答案:
3.B
4. 如图,每个小正方形的边长为 1,四边形的顶点 A,B,C,D 都在格点上,则下面 4 条线段长度为$\sqrt{10}$的是(
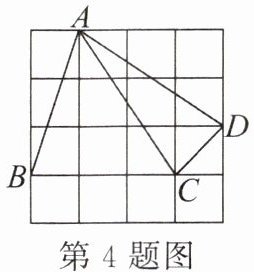
A.AB
B.BC
C.CD
D.AD
A
)
A.AB
B.BC
C.CD
D.AD
答案:
4.A
5. 如图,若两个正方形的面积分别为 64 和 49,则 AC =
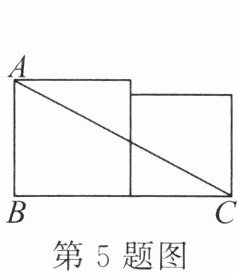
17
。
答案:
5.17
6. 已知:如图,在 Rt△ABC 中,∠ACB = 90°,AC = 15,BC = 20,CD 是斜边 AB 上的高。
(1) 求 AB 的长。
(2) 求 CD 的长。
 ]
]
(1) 求 AB 的长。
(2) 求 CD 的长。
 ]
]
答案:
6.解:
(1)在 Rt△ABC 中,
由勾股定理,得
AB = $\sqrt{AC^{2} + BC^{2}}$ = $\sqrt{15^{2} + 20^{2}}$ = 25;
(2)$S_{\triangle ABC}$ = $\frac{1}{2}$AC·BC = $\frac{1}{2}$AB·CD,
∴CD = $\frac{AC \cdot BC}{AB}$ = $\frac{15 × 20}{25}$ = 12.
∴斜边 AB 上的高 CD 为 12.
(1)在 Rt△ABC 中,
由勾股定理,得
AB = $\sqrt{AC^{2} + BC^{2}}$ = $\sqrt{15^{2} + 20^{2}}$ = 25;
(2)$S_{\triangle ABC}$ = $\frac{1}{2}$AC·BC = $\frac{1}{2}$AB·CD,
∴CD = $\frac{AC \cdot BC}{AB}$ = $\frac{15 × 20}{25}$ = 12.
∴斜边 AB 上的高 CD 为 12.
查看更多完整答案,请扫码查看


