7. 将方程 $(2x - 1)(3x + 1) = x^{2}+2$ 化成一般形式是
$5x^{2}-x-3=0$
.(二次项系数大于0)
答案:
$5x^{2}-x-3=0$
8. 方程 $(x - 1)^{2} = 2$ 的解是
$x_{1}=1+\sqrt {2},x_{2}=1-\sqrt {2}$
.
答案:
$x_{1}=1+\sqrt {2},x_{2}=1-\sqrt {2}$
9. 关于 $x$ 的一元二次方程 $x^{2}+bx - 10 = 0$ 的一个根为2,则 $b$ 的值为
3
.
答案:
3
10. 方程 $x^{2} - 4x + 1 = 0$ 的根的情况是
有两个不相等的实数根
.
答案:
有两个不相等的实数根
11. 若两个连续整数的积为210,则这两个数分别是
14,15或-15,-14
.
答案:
14,15或-15,-14
12. 如图,有一块长32cm、宽24cm的矩形纸片,在每个角上截去相同的小正方形,再折起来做成一个无盖的盒子. 已知盒子的底面积是原纸片面积的一半,则盒子的高为
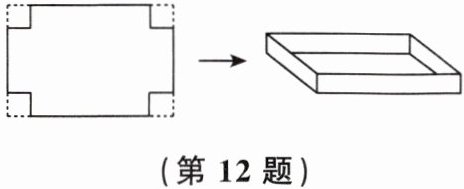
4 cm
.
答案:
4 cm
13.(每小题6分,共12分)解下列方程:
(1)$12(x - 3) = (x + 3)(x - 3)$;
(2)$2x^{2}+4x + 1 = 0$.
(1)$12(x - 3) = (x + 3)(x - 3)$;
(2)$2x^{2}+4x + 1 = 0$.
答案:
(1)$\because 12(x-3)=(x+3)(x-3),$$\therefore (x-3)(x-9)=0,$$\therefore x-3=0$或$x-9=0,$$\therefore x_{1}=3,x_{2}=9.$
(2)这里$a=2,b=4,c=1.$$\because \Delta =b^{2}-4ac=4^{2}-4×2×1=8,$$\therefore x=\frac {-4\pm \sqrt {8}}{2×2}=\frac {-2\pm \sqrt {2}}{2},$$\therefore x_{1}=\frac {-2+\sqrt {2}}{2},x_{2}=\frac {-2-\sqrt {2}}{2}.$
(1)$\because 12(x-3)=(x+3)(x-3),$$\therefore (x-3)(x-9)=0,$$\therefore x-3=0$或$x-9=0,$$\therefore x_{1}=3,x_{2}=9.$
(2)这里$a=2,b=4,c=1.$$\because \Delta =b^{2}-4ac=4^{2}-4×2×1=8,$$\therefore x=\frac {-4\pm \sqrt {8}}{2×2}=\frac {-2\pm \sqrt {2}}{2},$$\therefore x_{1}=\frac {-2+\sqrt {2}}{2},x_{2}=\frac {-2-\sqrt {2}}{2}.$
查看更多完整答案,请扫码查看


