16.(本题 10 分)如图,矩形 $ ABCD $ 在平面直角坐标系的第一象限内,$ BC $ 与 $ x $ 轴平行,$ AB = 1 $,点 $ C $ 的坐标为 $ (6,2) $,点 $ E $ 是 $ AD $ 的中点.反比例函数 $ y_1 = \frac{k}{x}(x > 0) $ 的图象经过点 $ C $ 和点 $ E $,过点 $ B $ 的直线 $ y_2 = ax + b $ 与反比例函数的图象交于点 $ F $,点 $ F $ 的纵坐标为 4.
(1)求反比例函数的表达式和点 $ E $ 的坐标;
(2)求直线 $ BF $ 的函数表达式;
(3)直接写出 $ y_1 > y_2 $ 时,自变量 $ x $ 的取值范围.
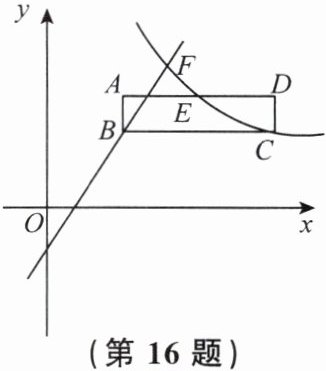
(1)求反比例函数的表达式和点 $ E $ 的坐标;
(2)求直线 $ BF $ 的函数表达式;
(3)直接写出 $ y_1 > y_2 $ 时,自变量 $ x $ 的取值范围.

答案:
解:
(1)
∵反比例函数$y_{1}=\frac{k}{x}(x>0)$的图象经过点C,点C的坐标为$(6,2)$,
∴$k=6× 2=12$, 即反比例函数的表达式为$y_{1}=\frac{12}{x}(x>0)$.
∵矩形ABCD在平面直角坐标系的第一象限内,BC与x轴平行,$AB=1$,点C的坐标为$(6,2)$,
∴点E的纵坐标是$2+1=3$, 把$y=3$代入$y_{1}=\frac{12}{x}$中得$x=4$, 即点E的坐标为$(4,3)$.
(2)
∵点E的坐标为$(4,3)$,点C的坐标为$(6,2)$,
∴$AE=DE=6 - 4=2$,
∴点A的坐标为$(2,3)$,
∴点B的横坐标为2, 即点B的坐标为$(2,2)$.
∵过点B的直线$y_{2}=ax+b$与反比例函数的图象交于点F,点F的纵坐标为4,
∴把$y=4$代入$y_{1}=\frac{12}{x}$中得$4=\frac{12}{x}$, 解得$x=3$, 即点F的坐标为$(3,4)$, 把点B,F的坐标代入$y_{2}=ax+b$中得$\begin{cases}2=2a+b,\\4=3a+b,\end{cases}$ 解得$\begin{cases}a=2,\\b=-2,\end{cases}$
∴直线BF的函数表达式为$y_{2}=2x - 2$.
(3)$0<x<3$.
(1)
∵反比例函数$y_{1}=\frac{k}{x}(x>0)$的图象经过点C,点C的坐标为$(6,2)$,
∴$k=6× 2=12$, 即反比例函数的表达式为$y_{1}=\frac{12}{x}(x>0)$.
∵矩形ABCD在平面直角坐标系的第一象限内,BC与x轴平行,$AB=1$,点C的坐标为$(6,2)$,
∴点E的纵坐标是$2+1=3$, 把$y=3$代入$y_{1}=\frac{12}{x}$中得$x=4$, 即点E的坐标为$(4,3)$.
(2)
∵点E的坐标为$(4,3)$,点C的坐标为$(6,2)$,
∴$AE=DE=6 - 4=2$,
∴点A的坐标为$(2,3)$,
∴点B的横坐标为2, 即点B的坐标为$(2,2)$.
∵过点B的直线$y_{2}=ax+b$与反比例函数的图象交于点F,点F的纵坐标为4,
∴把$y=4$代入$y_{1}=\frac{12}{x}$中得$4=\frac{12}{x}$, 解得$x=3$, 即点F的坐标为$(3,4)$, 把点B,F的坐标代入$y_{2}=ax+b$中得$\begin{cases}2=2a+b,\\4=3a+b,\end{cases}$ 解得$\begin{cases}a=2,\\b=-2,\end{cases}$
∴直线BF的函数表达式为$y_{2}=2x - 2$.
(3)$0<x<3$.
查看更多完整答案,请扫码查看


