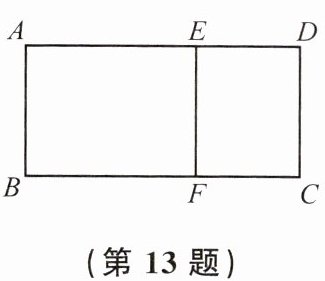
13. 如图,矩形ABCD中,点E,F分别在AD,BC边上,且$EF \perp BC$. 若四边形ABFE∽四边形DEFC,$AB = 4$,$AE = 5$,则DE的长为
16/5
.
答案:
16/5
14. 如图,把长为40cm、宽为30cm的长方形铁片的四角各剪去一个大小相同的正方形,然后折叠成一个无盖的长方体盒子,若铁盒的底面积(阴影部分)是原来铁片面积的一半,则盒子的高为

5
cm.
答案:
5
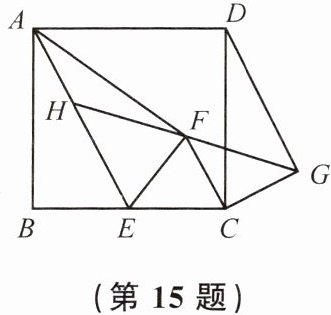
15. 如图,正方形ABCD中,点E是BC的中点,$\triangle ABE与\triangle AFE$关于AE所在直线对称,连接CF,将线段CF绕点C顺时针旋转$90^{\circ}$得到线段CG,连接DG,射线GF交AE于点H. 若$AB = 4$,则线段FH的长为
4√10/5
.
答案:
4√10/5
16. (每小题4分,共8分)用适当的方法解下列一元二次方程:
(1)$x^2 - 7x - 4 = 0$;
(2)$x(x + 2) = 4x + 8$.
(1)$x^2 - 7x - 4 = 0$;
(2)$x(x + 2) = 4x + 8$.
答案:
解:
(1)这里$a=1,b=-7,c=-4$,
$b^{2}-4ac=(-7)^{2}-4×1×(-4)=65>0$,
则$x=\frac{-(-7)\pm\sqrt{65}}{2×1}$,
所以,$x_{1}=\frac{7+\sqrt{65}}{2},x_{2}=\frac{7-\sqrt{65}}{2}$.
(2)方程右边分解因式,得$x(x+2)=4(x+2)$.
移项,得$x(x+2)-4(x+2)=0$.
方程左边分解因式,得$(x+2)(x-4)=0$.
所以,得$x+2=0$或$x-4=0$.
所以,$x_{1}=-2,x_{2}=4$.
(1)这里$a=1,b=-7,c=-4$,
$b^{2}-4ac=(-7)^{2}-4×1×(-4)=65>0$,
则$x=\frac{-(-7)\pm\sqrt{65}}{2×1}$,
所以,$x_{1}=\frac{7+\sqrt{65}}{2},x_{2}=\frac{7-\sqrt{65}}{2}$.
(2)方程右边分解因式,得$x(x+2)=4(x+2)$.
移项,得$x(x+2)-4(x+2)=0$.
方程左边分解因式,得$(x+2)(x-4)=0$.
所以,得$x+2=0$或$x-4=0$.
所以,$x_{1}=-2,x_{2}=4$.
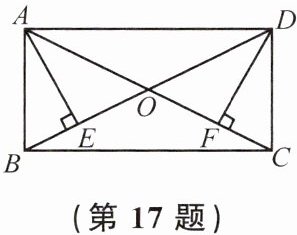
17. (本题5分)如图,在矩形ABCD中,对角线AC,BD相交于点O,过点A,D分别作BD,AC的垂线,垂足分别为点E,F.
求证:$AE = DF$.
求证:$AE = DF$.

答案:
证明:
∵四边形$ABCD$是矩形,
$\therefore AC=BD,OA=OC=\frac{1}{2}AC$,
$OD=OB=\frac{1}{2}BD$,
$\therefore OA=OD$.
∵$AE\perp BD$于点$E$,$DF\perp AC$于点$F$,
$\therefore \angle AEO=\angle DFO=90^{\circ}$.
$\because \angle AOE=\angle DOF$,
$\therefore \triangle AOE\cong \triangle DOF(AAS)$,
$\therefore AE=DF$.
∵四边形$ABCD$是矩形,
$\therefore AC=BD,OA=OC=\frac{1}{2}AC$,
$OD=OB=\frac{1}{2}BD$,
$\therefore OA=OD$.
∵$AE\perp BD$于点$E$,$DF\perp AC$于点$F$,
$\therefore \angle AEO=\angle DFO=90^{\circ}$.
$\because \angle AOE=\angle DOF$,
$\therefore \triangle AOE\cong \triangle DOF(AAS)$,
$\therefore AE=DF$.
查看更多完整答案,请扫码查看


