6. 如图,在矩形 $ABCD$ 中,点 $O$ 是 $AC$ 的中点,过点 $O$ 的直线分别与 $AB$,$CD$ 交于点 $E$,$F$,连接 $BF$ 交 $AC$ 于点 $M$,连接 $DE$,$BO$. 若 $\angle COB = 60^{\circ}$,$FO = FC$,有下列结论:
① $\triangle AOE \cong \triangle COF$;② $\triangle EOB \cong \triangle CMB$;③ $FB \perp OC$,$OM = CM$;④ 四边形 $EBFD$ 是菱形;⑤ $MB:OE = 3:2$. 其中正确的结论有(

A.5 个
B.4 个
C.3 个
D.2 个
① $\triangle AOE \cong \triangle COF$;② $\triangle EOB \cong \triangle CMB$;③ $FB \perp OC$,$OM = CM$;④ 四边形 $EBFD$ 是菱形;⑤ $MB:OE = 3:2$. 其中正确的结论有(
B
).
A.5 个
B.4 个
C.3 个
D.2 个
答案:
B
7. 已知四边形 $ABCD$ 是菱形,对角线的交点为 $O$. 若再补充一个条件能使四边形 $ABCD$ 成为正方形,则这个条件可以是
AC=BD(答案不唯一)
.(填写一个你认为适当的条件)
答案:
AC=BD(答案不唯一)
8. 如图,在菱形 $ABCD$ 中,对角线 $AC$ 与 $BD$ 相交于点 $O$,且 $AC = 8$,$BD = 6$,则菱形 $ABCD$ 的高 $DH = $
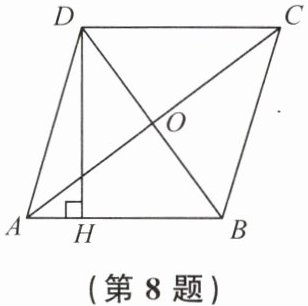
4.8
.
答案:
4,8
9. 如图,点 $D$ 在 $\triangle ABC$ 的边 $BC$ 上,$DE // AC$ 交 $AB$ 于点 $E$,$DF // AB$ 交 $AC$ 于点 $F$. 若添加条件
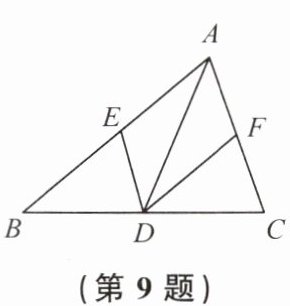
∠BAC=90°
,则四边形 $AEDF$ 是矩形;若添加条件AD平分∠BAC
,则四边形 $AEDF$ 是菱形;若添加条件∠BAC=90°且AD平分∠BAC
,则四边形 $AEDF$ 是正方形.
答案:
∠BAC=90° AD平分∠BAC ∠BAC=90°且AD平分∠BAC (答案不唯一)
10. 如图,在矩形 $ABCD$ 中,$\angle ABC$ 的平分线交 $AD$ 于点 $E$,连接 $CE$. 若 $BC = 7$,$AE = 4$,则 $CE = $
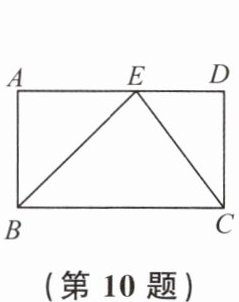
5
.
答案:
5
11. 如图,在平面直角坐标系中,矩形活动框架 $ABCD$ 的长 $AB = 2$,宽 $AD = \sqrt{2}$,其中边 $AB$ 在 $x$ 轴上,且原点 $O$ 为 $AB$ 的中点. 固定点 $A$,$B$,把这个矩形活动框架沿箭头方向推,使点 $D$ 落在 $y$ 轴的正半轴点 $D'$ 处,则点 $C$ 的对应点 $C'$ 的坐标为
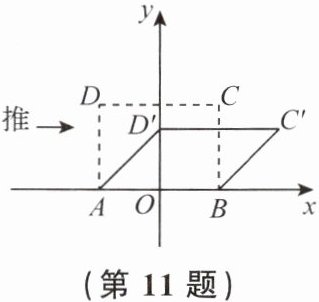
(2,1)
.
答案:
(2,1)
12. 如图,四边形 $ABCD$ 是菱形,$AB = 4$,且 $\angle ABC = \angle ABE = 60^{\circ}$,$M$ 为对角线 $BD$(不含点 $B$)上任意一点,将 $BM$ 绕点 $B$ 逆时针旋转 $60^{\circ}$ 得到 $BN$,连接 $EN$,$AM$,$CM$,则 $AM + BM + CM$ 的最小值为
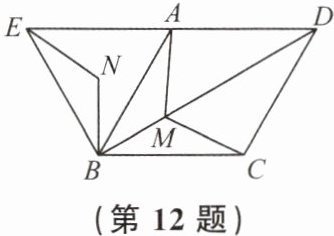
4√3
.
答案:
4√3
查看更多完整答案,请扫码查看


