搜索
11. 如图,在矩形$ABCD$中,点$E是AB$上的一点,且$AE:BE = 3:2$,$DA边上有一点F$,$EF = 18$,将矩形沿着$EF$翻折,使点$A落在BC上的点G$处,则矩形的宽为
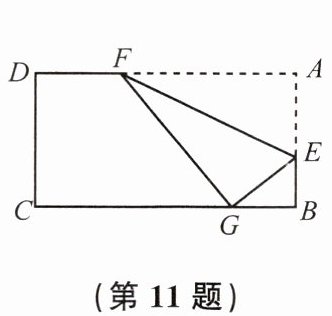
$5\sqrt{6}$
.
答案：
$5\sqrt{6}$
12. 如图,平面直角坐标系中,已知点$A(4,0)和点B(0,3)$,点$C是AB$的中点,若直线$CP截\triangle AOB所得的三角形与\triangle AOB$相似,那么点$P$的坐标是
$(0,\frac{3}{2}),(2,0),(\frac{7}{8},0)$
.
答案：
$(0,\frac{3}{2}),(2,0),(\frac{7}{8},0)$
13. (本题10分)如图,$\triangle ABC$在正方形方格纸中,$\triangle ABC$的顶点均在格点上. 请解答下列问题：
(1)请在正方形方格纸上建立平面直角坐标系,使点$A的坐标为(2,3)$,点$C的坐标为(6,2)$,并写出点$B$的坐标；
(2)以原点$O$为位似中心,相似比为2,在第一象限内将$\triangle ABC$放大,画出放大后的图形$\triangle A'B'C'$；
(3)计算$\triangle A'B'C'$的面积.
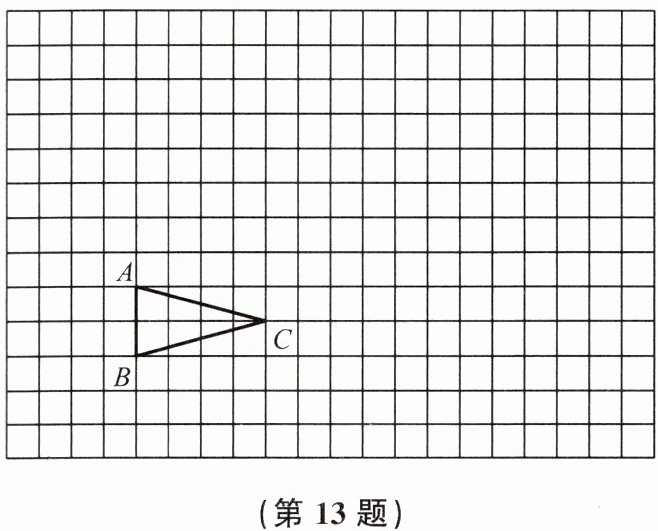
(1)请在正方形方格纸上建立平面直角坐标系,使点$A的坐标为(2,3)$,点$C的坐标为(6,2)$,并写出点$B$的坐标；
(2)以原点$O$为位似中心,相似比为2,在第一象限内将$\triangle ABC$放大,画出放大后的图形$\triangle A'B'C'$；
(3)计算$\triangle A'B'C'$的面积.
答案：
解:
(1)如图.
点 B 的坐标为$(2,1)$.
(2)如图,$\triangle A'B'C'$为所求.
(3)$S_{\triangle A'B'C'}=\frac{1}{2}×4×8=16$.
解:
(1)如图.
点 B 的坐标为$(2,1)$.(2)如图,$\triangle A'B'C'$为所求.
(3)$S_{\triangle A'B'C'}=\frac{1}{2}×4×8=16$.
查看更多完整答案，请扫码查看
