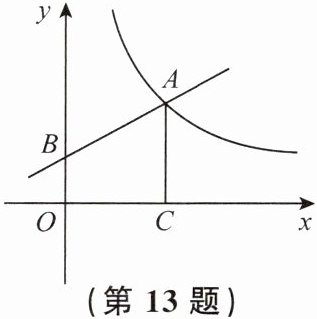
13.(本题 10 分)如图,已知点 $ A $ 在反比例函数 $ y = \frac{4}{x}(x > 0) $ 的图象上,过点 $ A $ 作 $ AC \perp x $ 轴,垂足是点 $ C $,$ AC = OC $.一次函数 $ y = kx + b $ 的图象经过点 $ A $,与 $ y $ 轴的正半轴交于点 $ B $.
(1)求点 $ A $ 的坐标;
(2)若四边形 $ ABOC $ 的面积是 3,求一次函数的表达式.
(1)求点 $ A $ 的坐标;
(2)若四边形 $ ABOC $ 的面积是 3,求一次函数的表达式.

答案:
解:
(1)
∵点A在反比例函数$y=\frac{4}{x}(x>0)$的图象上,$AC\perp x$轴,$AC=OC$,
∴$AC\cdot OC=4$,
∴$AC=OC=2$,
∴点A的坐标为$(2,2)$.
(2)
∵四边形ABOC的面积是3,
∴$(OB+2)× 2÷ 2=3$, 解得$OB=1$,
∴点B的坐标为$(0,1)$, 将点A,B的坐标分别代入一次函数$y=kx+b$,得$\begin{cases}2k+b=2,\\b=1,\end{cases}$ 解得$\begin{cases}k=\frac{1}{2},\\b=1,\end{cases}$ 故一次函数$y=kx+b$的表达式为$y=\frac{1}{2}x+1$.
(1)
∵点A在反比例函数$y=\frac{4}{x}(x>0)$的图象上,$AC\perp x$轴,$AC=OC$,
∴$AC\cdot OC=4$,
∴$AC=OC=2$,
∴点A的坐标为$(2,2)$.
(2)
∵四边形ABOC的面积是3,
∴$(OB+2)× 2÷ 2=3$, 解得$OB=1$,
∴点B的坐标为$(0,1)$, 将点A,B的坐标分别代入一次函数$y=kx+b$,得$\begin{cases}2k+b=2,\\b=1,\end{cases}$ 解得$\begin{cases}k=\frac{1}{2},\\b=1,\end{cases}$ 故一次函数$y=kx+b$的表达式为$y=\frac{1}{2}x+1$.
查看更多完整答案,请扫码查看


