1. 在等式 $x^{2}= 3$ 中,下列说法正确的是(
A.$x$ 是整数
B.$x$ 是分数
C.$x$ 是有理数
D.$x$ 不是有理数
D
)。A.$x$ 是整数
B.$x$ 是分数
C.$x$ 是有理数
D.$x$ 不是有理数
答案:
D
2. 正方形的面积为 10,则它的边长 $x$(
A.是分数
B.是有限小数
C.是整数
D.不是有理数
D
)。A.是分数
B.是有限小数
C.是整数
D.不是有理数
答案:
D
3. 下列正方形中,边长不是有理数的是(
A.面积为 64 的正方形
B.面积为 16 的正方形
C.面积为 1.44 的正方形
D.面积为 12 的正方形
D
)。A.面积为 64 的正方形
B.面积为 16 的正方形
C.面积为 1.44 的正方形
D.面积为 12 的正方形
答案:
D
4. 如图,在长方形 $ABCD$ 中,$AB = 3$,$BC = 5$,由勾股定理,可知 $AC^{2} = $
]
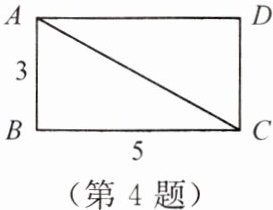
34
,而 $5^{2}$<
$AC^{2}$<
$6^{2}$(填“$>$”“$<$”或“$=$”),$AC$ 的长是介于整数5
与6
之间的一个数,而且这个数更接近整数6
。]

答案:
34 < < 5 6 6
5. 已知正数 $m$ 满足 $m^{2}= 39$,则 $m$ 的整数部分为
6
。
答案:
6
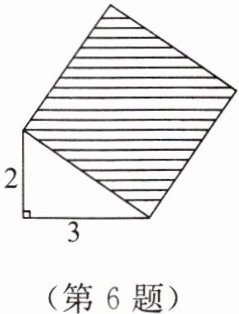
6. 如图,直角三角形两直角边的长分别是 2,3,阴影部分是一个正方形,设正方形的边长为 $a$。
(1)阴影部分的面积为多少?
(2)$a$ 是有理数吗?
]
(1)阴影部分的面积为多少?
(2)$a$ 是有理数吗?
]

答案:
(1)由勾股定理,得$a^{2}=2^{2}+3^{2}=13$,则阴影部分的面积为13。
(2)a不是有理数。
(1)由勾股定理,得$a^{2}=2^{2}+3^{2}=13$,则阴影部分的面积为13。
(2)a不是有理数。
7. 一个正方形的面积是 15,估计它的边长大小在(
A.2 和 3 之间
B.3 和 4 之间
C.4 和 5 之间
D.5 和 6 之间
B
)。A.2 和 3 之间
B.3 和 4 之间
C.4 和 5 之间
D.5 和 6 之间
答案:
B
8. 如图,网格中小正方形的边长都是 1,四边形 $ABCD$ 的四个顶点都在格点上,四条边中长度是有理数的有(
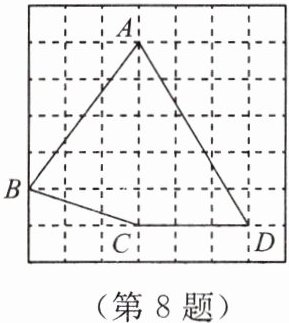
A.1 条
B.2 条
C.3 条
D.4 条
B
)。
A.1 条
B.2 条
C.3 条
D.4 条
答案:
B
9. 大家知道,当 $x^{2}= 2(x>0)$ 时,$x$ 的值不可能是有理数,而 $1^{2}<x^{2}<2^{2}$,所以 $x$ 的整数部分是 1。根据以上内容,解答下面的问题:
(1)若 $x^{2}= 10$,则 $x$ 的整数部分 $m = $
(2)若 $y^{2}= 17$,则 $y$ 的整数部分 $n = $
(3)若 $m$,$n$ 分别是一个三角形的两条边的长,第三条边的长是 5,则这个三角形是
(1)若 $x^{2}= 10$,则 $x$ 的整数部分 $m = $
3
;(2)若 $y^{2}= 17$,则 $y$ 的整数部分 $n = $
4
;(3)若 $m$,$n$ 分别是一个三角形的两条边的长,第三条边的长是 5,则这个三角形是
直角
三角形。
答案:
(1)3
(2)4
(3)直角
(1)3
(2)4
(3)直角
10. 已知直角三角形的两条直角边的长度分别是 9 cm 和 5 cm,斜边长是 $x$ cm。
(1)估计 $x$ 在哪两个整数之间。
(2)如果把 $x$ 的结果精确到十分位,估计 $x$ 的值;如果精确到百分位呢?用计算器验证你的估计值。
(1)估计 $x$ 在哪两个整数之间。
(2)如果把 $x$ 的结果精确到十分位,估计 $x$ 的值;如果精确到百分位呢?用计算器验证你的估计值。
答案:
解:根据条件,得$x^{2}=106$。
(1)因为100<106<121,所以$10^{2}<x^{2}<11^{2}$,所以x在整数10和11之间。
(2)因为$10.29^{2}=105.8841$,$10.30^{2}=106.09$,105.8841<106<106.09,所以$10.29^{2}<x^{2}<10.30^{2}$,所以当把x的结果精确到十分位时,$x≈10.3$。又因为$10.295^{2}=105.987025$,$10.296^{2}=106.007616$,105.987025<106<106.007616,所以$10.295^{2}<x^{2}<10.296^{2}$,所以把x的结果精确到百分位时,$x≈10.30$。用计算器验证略。
(1)因为100<106<121,所以$10^{2}<x^{2}<11^{2}$,所以x在整数10和11之间。
(2)因为$10.29^{2}=105.8841$,$10.30^{2}=106.09$,105.8841<106<106.09,所以$10.29^{2}<x^{2}<10.30^{2}$,所以当把x的结果精确到十分位时,$x≈10.3$。又因为$10.295^{2}=105.987025$,$10.296^{2}=106.007616$,105.987025<106<106.007616,所以$10.295^{2}<x^{2}<10.296^{2}$,所以把x的结果精确到百分位时,$x≈10.30$。用计算器验证略。
查看更多完整答案,请扫码查看


