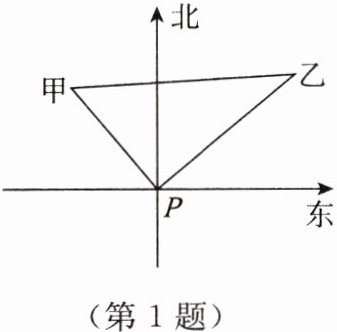
1. 如图,某港口$P$位于东西方向的海岸线上,甲、乙两艘轮船同时离开港口$P$,分别以每小时$12海里和16海里的速度沿着北偏西40^{\circ}方向和北偏东50^{\circ}$方向航行,$1$小时后,两船相距
]
20
海里。]

答案:
20
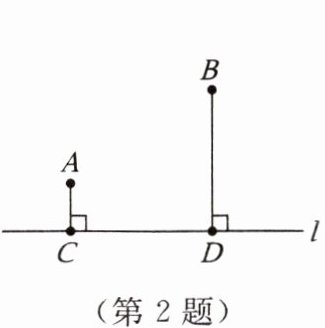
2. 如图,要在河边$l$上修建一座水泵站,分别向$A$,$B$两个村庄送水,已知$A$,$B两村到河边的距离分别为AC = 1km和BD = 3km$,且$C$,$D两点相距3km$,则所铺设的水管至少是(
A.$5km$
B.$4km$
C.$3km$
D.$6km$
A
)。
A.$5km$
B.$4km$
C.$3km$
D.$6km$
答案:
A
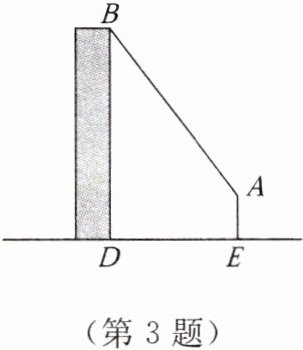
3. 如图,一高层住宅发生火灾,消防车立即赶到距高层住宅$9m$处(车尾$AE到高层住宅墙面的距离DE$),升起云梯$AB$到发生火灾的住户家窗口,已知云梯长$15m$,云梯底部距地面$3m$,发生火灾的住户家窗口距地面的高度$BD$是多少米?
]
]

答案:
解:过点A作$AC\perp BD$,垂足为C,如图,由题意可知$AE=CD=3\ m,AC=9\ m,AB=15\ m$,在$Rt\triangle ABC$中,根据勾股定理,得$AC^{2}+BC^{2}=AB^{2}$,即$9^{2}+BC^{2}=15^{2}$,所以$BC^{2}=15^{2}-9^{2}=144=12^{2}$,所以$BC=12\ m$,因此,$BD=BC+CD=12+3=15(m)$,所以发生火灾的住户家窗口距地面的高度BD是15 m。

解:过点A作$AC\perp BD$,垂足为C,如图,由题意可知$AE=CD=3\ m,AC=9\ m,AB=15\ m$,在$Rt\triangle ABC$中,根据勾股定理,得$AC^{2}+BC^{2}=AB^{2}$,即$9^{2}+BC^{2}=15^{2}$,所以$BC^{2}=15^{2}-9^{2}=144=12^{2}$,所以$BC=12\ m$,因此,$BD=BC+CD=12+3=15(m)$,所以发生火灾的住户家窗口距地面的高度BD是15 m。

查看更多完整答案,请扫码查看


