1. 如图,$a$,$b$,$c$分别表示以直角三角形的三条边为边分别向外作的正方形的面积,下列关系正确的是(

A.$a + b = c$
B.$a^{2} + b^{2} = c^{2}$
C.$ab = c$
D.$a + b = c^{2}$
]
A
)。
A.$a + b = c$
B.$a^{2} + b^{2} = c^{2}$
C.$ab = c$
D.$a + b = c^{2}$
]
答案:
A
2. 如图,点$A$,$C$之间隔有一湖,在与$AC方向成90^{\circ}角的CB方向上的点B处测得BA = 50\ m$,$BC = 40\ m$,则$A$,$C$两点之间的距离为(
A.$30\ m$
B.$40\ m$
C.$50\ m$
D.$60\ m$
]
A
)。
A.$30\ m$
B.$40\ m$
C.$50\ m$
D.$60\ m$
]
答案:
A
3. 如图,由四个全等的直角三角形拼成一个大正方形,若直角三角形的两条直角边长分别为$2$,$3$,则大正方形的面积为

13
。
答案:
13
4. 如图,阴影部分是两个正方形,其他三个图形是一个正方形和两个直角三角形,则阴影部分的面积为
]
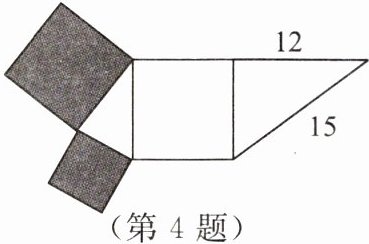
81
。]

答案:
81
5. 如图,直线$l上有三个正方形A$,$B$,$C$,若正方形$A$,$C的面积分别为5和11$,则正方形$B$的面积为(
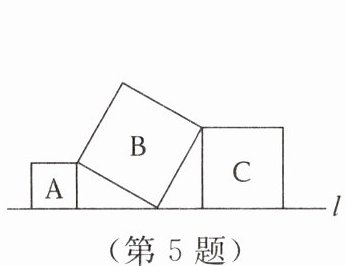
A.$4$
B.$6$
C.$16$
D.$55$
]
C
)。
A.$4$
B.$6$
C.$16$
D.$55$
]
答案:
C
6. 如图,在长方形$ABCD$中,点$E在边AB$上,将长方形$ABCD沿直线DE$折叠,点$A恰好落在边BC上的点F$处。若$AE = 5$,$BF = 3$,则$CD$的长为(

A.$7$
B.$8$
C.$9$
D.$10$
C
)。
A.$7$
B.$8$
C.$9$
D.$10$
答案:
C
7. 如图,$A地和B$地之间有一座山,从$A地到B地需要绕行C$地。在$\triangle ABC$中,$\angle C = 90^{\circ}$,$AC = 300\ m$,$BC = 400\ m$,若打通穿山隧道,建成$A$,$B$两地的高铁,则$AB = $
]

500
$m$,一辆全长$200\ m$的动车组,以$350\ km/h$的速度全部通过该隧道需要7.2
$s$。]

答案:
500 7.2
8. 【数学应用】我们发现,用不同的方式表示同一图形的面积可以解决线段长度之间关系的有关问题,这种方法称为等面积法,这是一种重要的数学方法。请你用等面积法来探究下列问题:
(1)图①是著名的“赵爽弦图”,由四个全等的直角三角形拼成,请你用它验证勾股定理;
(2)如图②,在$Rt\triangle ABC$中,$\angle ACB = 90^{\circ}$,$CD是AB$边上的高,$AC = 4$,$BC = 3$,求$CD$的长度;
(3)尝试构造一个图形,使它能够解释$(a + 2b)(a + b) = a^{2} + 3ab + 2b^{2}$,并在图中标注出$a$,$b$所表示的线段。

(1)图①是著名的“赵爽弦图”,由四个全等的直角三角形拼成,请你用它验证勾股定理;
(2)如图②,在$Rt\triangle ABC$中,$\angle ACB = 90^{\circ}$,$CD是AB$边上的高,$AC = 4$,$BC = 3$,求$CD$的长度;
(3)尝试构造一个图形,使它能够解释$(a + 2b)(a + b) = a^{2} + 3ab + 2b^{2}$,并在图中标注出$a$,$b$所表示的线段。

答案:
解:
(1)因为大正方形的面积为$c^{2}$,直角三角形的面积为$\frac{1}{2}ab$,小正方形的面积为$(b - a)^{2}$,所以$c^{2}=4×\frac{1}{2}ab+(b - a)^{2}=2ab+b^{2}-2ab+a^{2}$,即$c^{2}=a^{2}+b^{2}$。
(2)在$Rt\triangle ABC$中,因为$\angle ACB = 90^{\circ}$,所以由勾股定理,可得$AB^{2}=AC^{2}+BC^{2}=25$,所以$AB = 5$。
又因为$CD\perp AB$,所以$S_{\triangle ABC}=\frac{1}{2}AB\cdot CD=\frac{1}{2}AC\cdot BC$,所以$CD=\frac{12}{5}$。
(3)(答案不唯一,合理即可)如图,大长方形的面积既可以表示为$(a + b)(a + 2b)$,也可以表示为$a^{2}+3ab+2b^{2}$。因此,$(a + b)(a + 2b)=a^{2}+3ab+2b^{2}$。

解:
(1)因为大正方形的面积为$c^{2}$,直角三角形的面积为$\frac{1}{2}ab$,小正方形的面积为$(b - a)^{2}$,所以$c^{2}=4×\frac{1}{2}ab+(b - a)^{2}=2ab+b^{2}-2ab+a^{2}$,即$c^{2}=a^{2}+b^{2}$。
(2)在$Rt\triangle ABC$中,因为$\angle ACB = 90^{\circ}$,所以由勾股定理,可得$AB^{2}=AC^{2}+BC^{2}=25$,所以$AB = 5$。
又因为$CD\perp AB$,所以$S_{\triangle ABC}=\frac{1}{2}AB\cdot CD=\frac{1}{2}AC\cdot BC$,所以$CD=\frac{12}{5}$。
(3)(答案不唯一,合理即可)如图,大长方形的面积既可以表示为$(a + b)(a + 2b)$,也可以表示为$a^{2}+3ab+2b^{2}$。因此,$(a + b)(a + 2b)=a^{2}+3ab+2b^{2}$。

查看更多完整答案,请扫码查看


