《2025年课堂精练八年级数学上册北师大版福建专版》

3. 如图,在平面直角坐标系中,$\triangle ABO的顶点A的坐标为(-3,-3)$,顶点$B的坐标为(-3,4)$,点$P为线段AB$上任意一点(不与点$A$,$B$重合),点$Q是点P关于x$轴对称的点。
(1) 求$\triangle ABO$的面积；
(2) 若点$P的纵坐标为n$,则点$Q$的坐标为____(-3,-n)；
(3) 当$\triangle OPA的面积是\triangle OPQ面积的2$倍时,求点$P$的坐标。

3.解:
(1)根据题意得AB=4-(-3)=7,所以S△ABO=1/2×7×3=21/2。
(2)(-3,-n)　
(3)因为S△OPA=2S△OPQ,点O到AB的距离为3,所以AP=2PQ。又因为AP=n-(-3)=n+3,PQ=|n-(-n)|=|2n|,所以n+3=4n或n+3=-4n,解得n=1或n=-3/5。因此，点P的坐标为(-3,1)或(-3,-3/5)。

答案： 3.解:
(1)根据题意得AB=4-(-3)=7,所以S△ABO=1/2×7×3=21/2。
(2)(-3,-n)　
(3)因为S△OPA=2S△OPQ,点O到AB的距离为3,所以AP=2PQ。又因为AP=n-(-3)=n+3,PQ=|n-(-n)|=|2n|,所以n+3=4n或n+3=-4n,解得n=1或n=-3/5。因此，点P的坐标为(-3,1)或(-3,-3/5)。

4. 如图,在平面直角坐标系中,$O$是原点,已知点$A的坐标为(4,3)$,$P$是坐标轴上一点。若由$O$,$A$,$P$三点组成的三角形为等腰三角形,则满足条件的点$P$共有8个,其中一个点$P$的坐标是(-5,0)。

答案： 4.8　(-5,0)(第二个空答案不唯一)

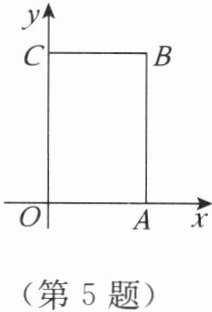
5. 如图,在长方形OABC中,O为平面直角坐标系的原点,点A的坐标为(a,0),点C的坐标为(0,b),且a,b满足$\sqrt{a - 4}+\vert b - 6\vert = 0,$点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿O - C - B - A - O的路线移动。
(1) 点B的坐标为(4,6)；当点P移动3.5s时,点P的坐标为(1,6)。
(2) 在移动过程中,当点P到x轴的距离为4个单位长度时,求点P移动的时间。
在移动过程中，当点P到x轴的距离为4个单位长度时，存在两种情况:①当点P在OC上时，OP=4,移动的时间为4÷2=2(s);②当点P在AB上时,AP=4,点P运动的路程为6+4+6-4=12,移动的时间为12÷2=6(s)。所以在移动过程中，当点P到x轴的距离为4个单位长度时，点P移动的时间为2s或6s。
(3) 当点P沿着O - C - B的路线移动时,是否存在某一时刻使$\triangle OBP$的面积为10？若存在,求出点P移动的时间；若不存在,请说明理由。
存在。当点P在OC上时,1/2 OP·BC=1/2×2t×4=10,解得t=5/2;当点P在BC上时,1/2 BP·OC=1/2×(10-2t)×6=10,解得t=10/3。因此，当点P移动的时间为5/2s或10/3s时,△OBP的面积为10。

答案： 5.解:
(1)(4,6)　(1,6)　
(2)在移动过程中，当点P到x轴的距离为4个单位长度时，存在两种情况:①当点P在OC上时，OP=4,移动的时间为4÷2=2(s);②当点P在AB上时,AP=4,点P运动的路程为6+4+6-4=12,移动的时间为12÷2=6(s)。所以在移动过程中，当点P到x轴的距离为4个单位长度时，点P移动的时间为2s或6s。　
(3)存在。当点P在OC上时,1/2 OP·BC=1/2×2t×4=10,解得t=5/2;当点P在BC上时,1/2 BP·OC=1/2×(10-2t)×6=10,解得t=10/3。因此，当点P移动的时间为5/2s或10/3s时,△OBP的面积为10。