1. 若函数 $ y = kx $ 的图象经过点 $(1,-2)$,则它一定经过点(
A.$(2,-1)$
B.$\left(-\frac{1}{2},1\right)$
C.$(-2,1)$
D.$\left(-1,\frac{1}{2}\right)$
B
)。A.$(2,-1)$
B.$\left(-\frac{1}{2},1\right)$
C.$(-2,1)$
D.$\left(-1,\frac{1}{2}\right)$
答案:
B
2. 已知一次函数 $ y = kx + b $,当 $ x = 1 $ 时,$ y = 2 $,且它的图象与 $ y $ 轴交点的纵坐标是 3,则此函数的表达式为(
A.$ y = x + 3 $
B.$ y = x - 3 $
C.$ y = -x + 3 $
D.$ y = -x - 3 $
C
)。A.$ y = x + 3 $
B.$ y = x - 3 $
C.$ y = -x + 3 $
D.$ y = -x - 3 $
答案:
C
3. 如图,直线 $ y = kx + b $ 经过点 $ A,B $,则 $ k $ 的值为(
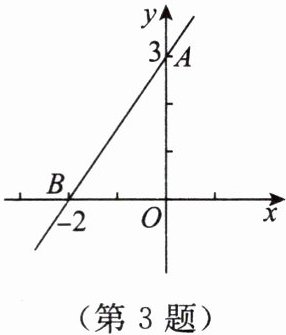
A.3
B.$\frac{3}{2}$
C.$\frac{2}{3}$
D.$-\frac{3}{2}$
B
)。
A.3
B.$\frac{3}{2}$
C.$\frac{2}{3}$
D.$-\frac{3}{2}$
答案:
B
4. 一次函数的图象经过点 $ A(-2,-1) $,且与直线 $ y = 2x - 3 $ 平行,则此函数的表达式为(
A.$ y = x + 3 $
B.$ y = 2x + 3 $
C.$ y = 2x - 3 $
D.$ y = -2x - 5 $
B
)。A.$ y = x + 3 $
B.$ y = 2x + 3 $
C.$ y = 2x - 3 $
D.$ y = -2x - 5 $
答案:
B
5. 一次函数 $ y = mx + |m - 1| $ 的图象过点 $(0,2)$,且 $ y $ 的值随着 $ x $ 值的增大而增大,则 $ m $ 的值为(
A.$-1$
B.3
C.1
D.$-1$ 或 3
B
)。A.$-1$
B.3
C.1
D.$-1$ 或 3
答案:
B
6. 写出一个同时具备下列两个条件的一次函数的表达式:
① $ y $ 的值随着 $ x $ 值的增大而减小;
② 图象经过点 $(0,3)$。
y=-x+3(答案不唯一)
。① $ y $ 的值随着 $ x $ 值的增大而减小;
② 图象经过点 $(0,3)$。
答案:
y=-x+3(答案不唯一)
7. 已知一次函数 $ y = -x + 3 $,当 $ 0 \leq x \leq 2 $ 时,$ y $ 的最大值是
3
。
答案:
3
8. 如图所示的是一次函数 $ y = kx + b $ 的图象,完成下列各题:
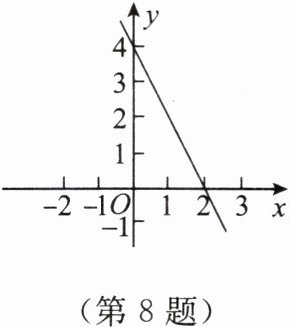
(1)当 $ x = 0 $ 时,$ y = $
(2)$ k = $
(3)当 $ x = 5 $ 时,$ y = $

(1)当 $ x = 0 $ 时,$ y = $
4
;当 $ x = $2
时,$ y = 0 $。(2)$ k = $
-2
,$ b = $4
。(3)当 $ x = 5 $ 时,$ y = $
-6
;当 $ y = 30 $ 时,$ x = $-13
。
答案:
(1)4 2
(2)-2 4
(3)-6 -13
(1)4 2
(2)-2 4
(3)-6 -13
9. 已知一次函数 $ y = 2x + m $ 的图象和 $ y = -x + n $ 的图象都经过点 $ A(-2,0) $,且与 $ y $ 轴分别交于 $ B,C $ 两点,则 $ \triangle ABC $ 的面积是(
A.2
B.3
C.4
D.6
D
)。A.2
B.3
C.4
D.6
答案:
D
10. 将 $ 6 × 6 $ 的正方形网格放置在如图所示的平面直角坐标系中,每个小正方形的顶点称为格点,每个小正方形的边长都是 1,正方形 $ ABCD $ 的顶点都在格点上。若直线 $ y = kx(k \neq 0) $ 与正方形 $ ABCD $ 有公共点,则 $ k $ 不可能是(
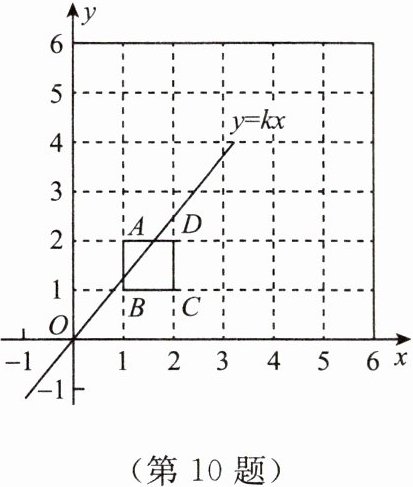
A.3
B.2
C.1
D.$\frac{1}{2}$
A
)。
A.3
B.2
C.1
D.$\frac{1}{2}$
答案:
A
查看更多完整答案,请扫码查看


