12. (1)点 $ P $ 的坐标为 $ (x,y) $,若 $ x = y $,则点 $ P $ 在坐标平面内的位置是
(2)已知点 $ Q $ 的坐标为 $ (2 - 2a,a + 8) $,且点 $ Q $ 到两坐标轴的距离相等,则点 $ Q $ 的坐标为
在第一、三象限的角平分线上
;若 $ x + y = 0 $,则点 $ P $ 在坐标平面内的位置是在第二、四象限的角平分线上
。(2)已知点 $ Q $ 的坐标为 $ (2 - 2a,a + 8) $,且点 $ Q $ 到两坐标轴的距离相等,则点 $ Q $ 的坐标为
(6,6)或(-18,18)
。
答案:
(1)在第一、三象限的角平分线上 在第二、四象限的角平分线上
(2)(6,6)或(-18,18)
(1)在第一、三象限的角平分线上 在第二、四象限的角平分线上
(2)(6,6)或(-18,18)
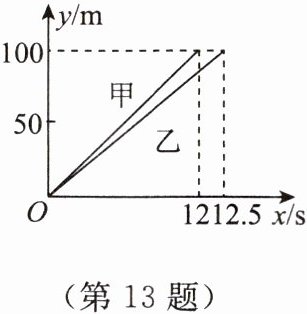
13. 如图所示的是甲、乙两人在一次赛跑中路程 $ y(m) $ 与时间 $ x(s) $ 之间的关系,看图回答下列问题:
(1)这是一次多少米的赛跑?
(2)谁先到达终点?
(3)乙在这次赛跑中的速度是多少?
(4)分别求甲、乙两人的路程与时间之间的关系式。
]
(1)这是一次多少米的赛跑?
(2)谁先到达终点?
(3)乙在这次赛跑中的速度是多少?
(4)分别求甲、乙两人的路程与时间之间的关系式。
]

答案:
解:
(1)这是一次100m的赛跑。
(2)甲先到达终点。
(3)乙在这次赛跑中的速度是100÷12.5=8(m/s)。
(4)设甲的路程与时间之间的关系式为y=k₁x,把x=12,y=100代入,得100=12k₁,k₁=$\frac{25}{3}$。所以甲的路程与时间之间的关系式为y=$\frac{25}{3}$x(0≤x≤12)。设乙的路程与时间之间的关系式为y=k₂x,把x=12.5,y=100代入,得100=12.5k₂,k₂=8。所以乙的路程与时间之间的关系式为y=8x(0≤x≤12.5)。
(1)这是一次100m的赛跑。
(2)甲先到达终点。
(3)乙在这次赛跑中的速度是100÷12.5=8(m/s)。
(4)设甲的路程与时间之间的关系式为y=k₁x,把x=12,y=100代入,得100=12k₁,k₁=$\frac{25}{3}$。所以甲的路程与时间之间的关系式为y=$\frac{25}{3}$x(0≤x≤12)。设乙的路程与时间之间的关系式为y=k₂x,把x=12.5,y=100代入,得100=12.5k₂,k₂=8。所以乙的路程与时间之间的关系式为y=8x(0≤x≤12.5)。
14. 【综合与实践】某班数学兴趣小组对函数 $ y = |x| $ 的图象和性质进行了探究,过程如下,请补充完整。
(1)自变量 $ x $ 的取值范围是全体实数,$ x $ 与 $ y $ 的几组对应值列表如下:
| $ x $ | …$ $ | $ -3 $ | $ -2 $ | $ -1 $ | $ 0 $ | $ 1 $ | $ 2 $ | $ 3 $ | $ 4 $ | $ 5 $ | …$ $ |
| $ y $ | …$ $ | $ 3 $ | $ m $ | $ 1 $ | $ 0 $ | $ 1 $ | $ 2 $ | $ 3 $ | $ 4 $ | $ 5 $ | …$ $ |

其中,$ m = $____。
(2)根据上表的数据,小组成员在如图所示的平面直角坐标系中描点,并画出了函数图象的一部分,请你画出该函数图象的另一部分。
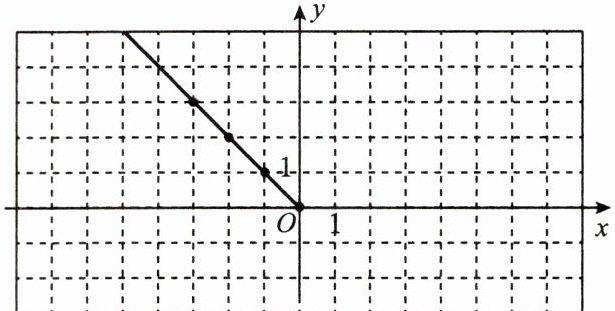
(3)观察图象,写出该函数的一条性质:____。
]
(1)自变量 $ x $ 的取值范围是全体实数,$ x $ 与 $ y $ 的几组对应值列表如下:
| $ x $ | …$ $ | $ -3 $ | $ -2 $ | $ -1 $ | $ 0 $ | $ 1 $ | $ 2 $ | $ 3 $ | $ 4 $ | $ 5 $ | …$ $ |
| $ y $ | …$ $ | $ 3 $ | $ m $ | $ 1 $ | $ 0 $ | $ 1 $ | $ 2 $ | $ 3 $ | $ 4 $ | $ 5 $ | …$ $ |

其中,$ m = $____。
(2)根据上表的数据,小组成员在如图所示的平面直角坐标系中描点,并画出了函数图象的一部分,请你画出该函数图象的另一部分。

(3)观察图象,写出该函数的一条性质:____。
]
答案:
(1)2
(2)函数图象如图所示。
(3)(答案不唯一,合理即可)函数值y≥0或当x>0时,y的值随着x值的增大而增大
(1)2
(2)函数图象如图所示。

(3)(答案不唯一,合理即可)函数值y≥0或当x>0时,y的值随着x值的增大而增大
查看更多完整答案,请扫码查看


