9. 如图,某人驱车在离 $A$ 地 $10km$ 的 $P$ 地出发,向 $B$ 地匀速行驶,$30min$ 后离 $P$ 地 $50km$,设出发 $x h$ 后,汽车离 $A$ 地 $y km$(未到达 $B$ 地前),则 $y$ 与 $x$ 之间的关系式为(

A.$y = 50x$
B.$y = 100x$
C.$y = 50x - 10$
D.$y = 100x + 10$
D
)。
A.$y = 50x$
B.$y = 100x$
C.$y = 50x - 10$
D.$y = 100x + 10$
答案:
D
10. 一支蜡烛长 $20cm$,每分钟燃烧的长度是 $2cm$,蜡烛剩余长度 $y(cm)$ 与燃烧时间 $x(min)$ 之间的关系式为
y=20-2x
。
答案:
y=20-2x
11. 周长为 $10cm$ 的等腰三角形,腰长 $y(cm)$ 与底边长 $x(cm)$ 之间的关系式为
$y=5-\dfrac{1}{2}x$
,自变量的取值范围是$0<x<5$
。
答案:
$y=5-\dfrac{1}{2}x 0<x<5$
12. 如图,正方形 $ABCD$ 的边长为 $4$,点 $P$ 是正方形边上的一个动点,以 $C$ 为起点,沿 $C - B - A$ 的路径移动,设点 $P$ 经过的路径长为 $x$,$\triangle APD$ 的面积为 $y$,则 $y$ 与 $x$ 之间的关系式为
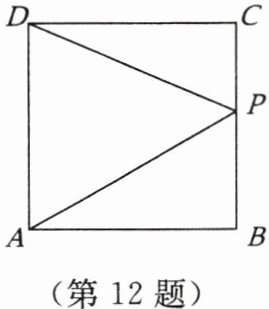
$y=\begin{cases} 8(0\leqslant x<4), \\ -2x+16(4\leqslant x<8) \end{cases}$
。
答案:
$y=\begin{cases} 8(0\leqslant x<4), \\ -2x+16(4\leqslant x<8) \end{cases}$
13.【数学应用】某商店出售一种瓜子,其售价 $y$(元) 与瓜子的质量 $x(kg)$ 之间的关系如下表:
|瓜子的质量 $x/kg$|1|2|3|4|…|
|售价 $y/$ 元|$20 + 0.2$|$40 + 0.2$|$60 + 0.2$|$80 + 0.2$|…|
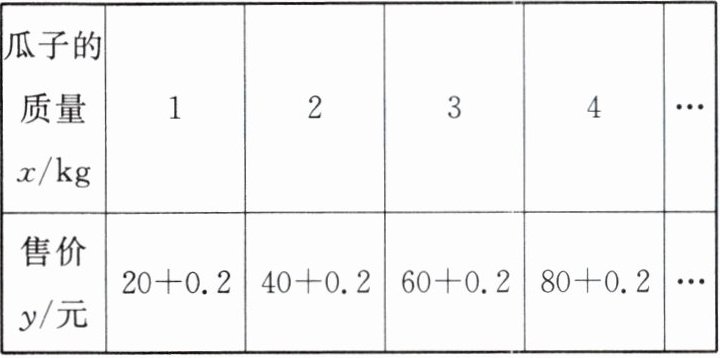
其中,售价中的 $0.2$ 元是包装的费用。
(1) 在这个变化过程中,自变量与因变量各是什么?
(2) 写出出售 $7kg$ 瓜子的售价。
(3) 写出 $y$ 与 $x$ 之间的关系式。
(4) 商店规定,当一次性购买 $100kg$ 及以上瓜子时,全部所购瓜子打九折。八(1) 班、八(2) 班正好要举办一次“党庆活动”,两个班一共 $94$ 人,每人购买 $1kg$,包装费用全免。要买够两个班的瓜子,最少要花多少钱?
|瓜子的质量 $x/kg$|1|2|3|4|…|
|售价 $y/$ 元|$20 + 0.2$|$40 + 0.2$|$60 + 0.2$|$80 + 0.2$|…|

其中,售价中的 $0.2$ 元是包装的费用。
(1) 在这个变化过程中,自变量与因变量各是什么?
(2) 写出出售 $7kg$ 瓜子的售价。
(3) 写出 $y$ 与 $x$ 之间的关系式。
(4) 商店规定,当一次性购买 $100kg$ 及以上瓜子时,全部所购瓜子打九折。八(1) 班、八(2) 班正好要举办一次“党庆活动”,两个班一共 $94$ 人,每人购买 $1kg$,包装费用全免。要买够两个班的瓜子,最少要花多少钱?
答案:
解:
(1)根据题意可知,在这个变化过程中,自变量是瓜子的质量,因变量是售价。
(2)根据题意得20×7+0.2=140+0.2=140.2(元),
所以出售7 kg瓜子的售价为140.2元。
(3)y=20x+0.2。
(4)当购买94 kg瓜子时所需要的费用为20×94=1880(元),
当购买100 kg瓜子时所需要的费用为20×0.9×100=1800(元),
1880>1800,
所以要买够两个班的瓜子,最少要花1800元。
(1)根据题意可知,在这个变化过程中,自变量是瓜子的质量,因变量是售价。
(2)根据题意得20×7+0.2=140+0.2=140.2(元),
所以出售7 kg瓜子的售价为140.2元。
(3)y=20x+0.2。
(4)当购买94 kg瓜子时所需要的费用为20×94=1880(元),
当购买100 kg瓜子时所需要的费用为20×0.9×100=1800(元),
1880>1800,
所以要买够两个班的瓜子,最少要花1800元。
查看更多完整答案,请扫码查看


