《2025年精彩练习就练这一本九年级数学全一册浙教版评议教辅》

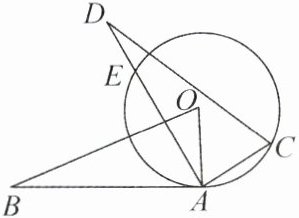
16. 如图,$\odot O与\triangle OAB$的边AB相切,切点为A. 将$\triangle OAB$绕点A按顺时针方向旋转得到$\triangle CAD$(点C与点O对应),使点C落在$\odot O$上,边AD交$\odot O$于点E. 若$OA= 2$,$AB= 3\sqrt{3}$,则DE的长为$\sqrt{3}$.

答案： $\sqrt{3}$

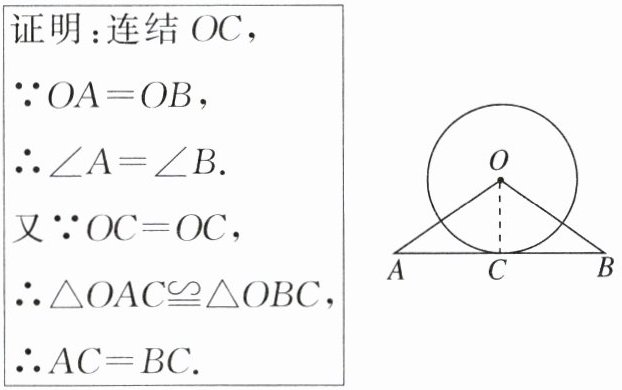
17. (8分)已知：如图,在$\triangle OAB$中,$OA= OB$,$\odot O$与AB相切于点C. 求证：$AC= BC$. 小明同学的证明过程如下框：

答案： 解:证法错误. 证明:连结OC(图略).
∵⊙O与AB相切于点C,
∴OC⊥AB.
∵OA=OB,
∴AC=BC.

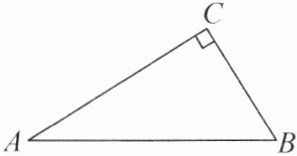
18. (8分)如图,在$\triangle ABC$中,$\angle ACB= 90^\circ$,$BC= \sqrt{5}$,$AC= 2\sqrt{5}$,
(1)若$\odot C$切AB于D,求$\odot C$的半径及切线AD的长.
(2)直接写出$\odot C$与线段AB有两个公共点时半径r的取值范围.

答案： 解:
(1)作CD⊥AB于D.(图略) 在△ABC中,∠ACB=90°,BC=$\sqrt{5}$,AC=2$\sqrt{5}$, 由勾股定理得AB=5,
∴$\frac{1}{2}$AC·BC=$\frac{1}{2}$AB·CD, 解得CD=2,即⊙C的半径为2. 在Rt△ADC中,AD²=AC²-CD², 即AD²=(2$\sqrt{5}$)²-2²,解得AD=4.
(2)
∵CD=2,BC=$\sqrt{5}$,
∴⊙C与线段AB有两个公共点时,2＜r≤$\sqrt{5}$.

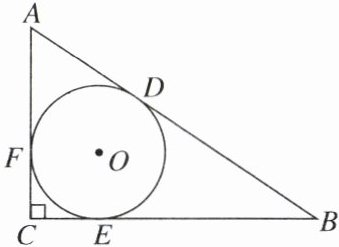
19. (8分)如图,在Rt$\triangle ABC$中,$\angle C= 90^\circ$,$\triangle ABC的内切圆为\odot O$,它切AB于点D,切BC于点E,切AC于点F,$AD= 4$,$BD= 6$,求Rt$\triangle ABC$的面积.

答案： 解:连结OE,OF,OD(图略). 设⊙O的半径为r.
∵⊙O切AB于点D,切BC于点E,切AC于点F,
∴∠OFC=∠OEC=∠C=90°,AF=AD=4,BD=BE=6,
∴四边形OECF是矩形.
∵OE=OF,
∴四边形OECF是正方形. 在Rt△ABC中,AB²=BC²+AC²,
∴10²=(6+r)²+(4+r)², 解得r=2或r=-12(舍去),
∴BC=8,AC=6,
∴Rt△ABC的面积=$\frac{1}{2}$×6×8=24.

20. (8分)已知AB是$\odot O$的直径,$AD\perp l$于点D.
(1)如图1,当直线l与$\odot O$相切于点C时,若$\angle DAC= 30^\circ$,求$\angle BAC$的大小.
(2)如图2,当直线l与$\odot O$相交于点E,F时,若$\angle DAE= 18^\circ$,求$\angle BAF$的大小.

答案：
解:
(1)如图1,连结OC.
∵l是⊙O的切线,
∴OC⊥l.
∵AD⊥l,
∴OC//AD,
∴∠OCA=∠DAC=30°.
∵OA=OC,
∴∠BAC=∠OCA=30°.
(2)如图2,连结BE.
∵AB是⊙O的直径,
∴∠AEB=90°,
∴∠AED+∠BEF=90°.
∵∠AED+∠DAE=90°,
∴∠BEF=∠DAE=18°.
∵⌒BF=⌒BF,
∴∠BAF=∠BEF=18°.