《2025年精彩练习就练这一本九年级数学全一册浙教版评议教辅》

18. (8分)如图,这是从一副扑克牌中取出的两组牌,分别是红桃1,2,3和方块1,2,3,将它们的背面朝上分别重新洗牌后,再从两组牌中各摸出一张.
(1)用列举法列举出所有可能出现的结果.
(2)求摸出的两张牌的牌面数字之和不小于5的概率.

答案： 解：
(1)(1,1)，(1,2)，(1,3)，(2,1)，(2,2)，(2,3)，(3,1)，(3,2)，(3,3)，共9种情况。
(2)摸出的两张牌的牌面数字之和不小于5的有(2,3)，(3,2)，(3,3)，
∴摸出的两张牌的牌面数字之和不小于5的概率为$\frac{3}{9}=\frac{1}{3}$。

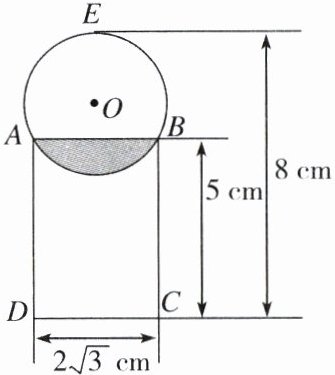
19. (8分)将一个球放在圆柱形塑料管上,它的横截面如下,测得有关数据如下图所示.求：
(1)该球的半径.
(2)阴影部分的面积.

答案： 解：
(1)过点O作$OF⊥AB$，垂足为F，连结OB，OE，如图。
根据垂径定理，由$AB = 2\sqrt{3}cm$，得$BF = \sqrt{3}cm$。
设半径为$x cm$，则$OB = x cm$。
∵$OF = 8 - 5 - x = 3 - x(cm)$，$OE = x cm$，
∴$OF = (3 - x)cm$。
在$Rt△OBF$中，$OF^{2}+BF^{2}=OB^{2}$，
∴$(3 - x)^{2}+(\sqrt{3})^{2}=x^{2}$，
∴$x = 2$，
∴该球的半径为2cm。
(2)在$Rt△OBF$中，
∵$OF = 3 - 2 = 1(cm)$，$OB = 2cm$，易得$∠BOF = 60°$。
∵$∠AOB = 2∠BOF = 2×60° = 120°$，
∴$S_{阴影}=S_{扇形OAB}-S_{△OAB}=\frac{4π}{3}-\sqrt{3}(cm^{2})$。

20. (8分)已知二次函数$y= (x+m)(x-1)$的图象经过点(2,-3).
(1)求这个二次函数的表达式.
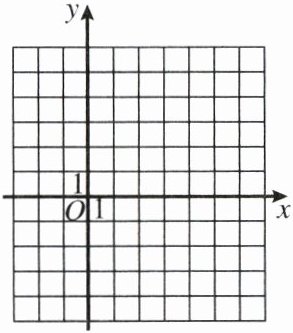
(2)在图中画出这个函数的图象,并利用图象解决下列问题：
①直接写出方程$(x+m)(x-1)= -3$的解.
②当x满足什么条件时,y＞0？

答案： 解：
(1)将点$(2,-3)$的坐标代入$y = (x + m)(x - 1)$，解得$m = - 5$，
故二次函数的表达式为$y = (x - 5)(x - 1)=x^{2}-6x + 5$。
(2)从函数的表达式看，函数图象的对称轴为直线$x = 3$，则点$(2,-3)$的对称点为$(4,-3)$，抛物线和y轴的交点为$(0,5)$，抛物线与x轴的交点为$(1,0)$，$(5,0)$。
根据上述5个点，描点、连线，绘制函数图象，如图。
①从图象看，直线$y = - 3$和抛物线的交点的横坐标为$x = 2$和$x = 4$，即方程$(x + m)(x - 1)= - 3$的解为$x = 2$或$x = 4$。
②从图象看，当$x＜1$或$x＞5$时，$y＞0$。

21. (8分)如图,四边形ABCD内接于⊙O,延长AB,DC交于点E,DE= DA.
(1)求证：△BCE是等腰三角形.
(2)若C是$\widehat{BD}$的中点,AB= 11,BC= 4,求AD的长.

答案： 解：
(1)证明：
∵$DE = DA$，
∴$∠E = ∠A$。
∵$∠A + ∠BCD = 180°$，$∠BCE + ∠BCD = 180°$，
∴$∠A = ∠BCE$，
∴$∠E = ∠BCE$，
∴$BE = CB$，
∴$△BCE$是等腰三角形。
(2)
∵C是$\widehat{BD}$的中点，
∴$DC = BC = 4$。
∵$BE = CB$，$AB = 11$，
∴$AE = 15$。
设$AD = ED = m$，则$CE = m - 4$。
∵$∠A = ∠BCE$，$∠AED = ∠CEB$，
∴$△DAE∽△BCE$，
∴$\frac{AD}{BC}=\frac{AE}{CE}$，即$\frac{m}{4}=\frac{15}{m - 4}$，
解得$m = 10$或$m = - 6$(舍去)。
∴$AD$的长为10。