18.(8分)如图,在Rt△ABC中,∠C= 90°,AC= 2,AB= 3.
(1)求BC的长.
(2)求sin A的值.

(1)求BC的长.
(2)求sin A的值.

答案:
解:
(1)在Rt△ABC中,∠C=90°,AC=2,AB=3,
∴BC=$\sqrt{AB²−AC²}$=$\sqrt{3²−2²}$=$\sqrt{5}$.
(2)在Rt△ABC中,∠C=90°,AB=3,BC=$\sqrt{5}$,
∴sinA=$\frac{BC}{AB}$=$\frac{\sqrt{5}}{3}$.
(1)在Rt△ABC中,∠C=90°,AC=2,AB=3,
∴BC=$\sqrt{AB²−AC²}$=$\sqrt{3²−2²}$=$\sqrt{5}$.
(2)在Rt△ABC中,∠C=90°,AB=3,BC=$\sqrt{5}$,
∴sinA=$\frac{BC}{AB}$=$\frac{\sqrt{5}}{3}$.
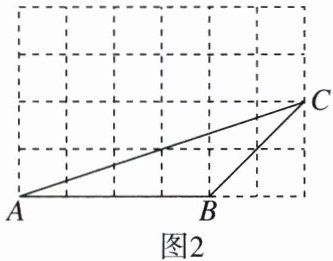
19.(8分)如图,在4×6的网格中,△ABC的顶点都在边长为1的小正方形的顶点上.
(1)∠CAB的正切值为______.
(2)分别在图1和图2中各画一个格点三角形,使得所画的三角形和△ABC相似且不全等(所画的两个三角形也不全等).

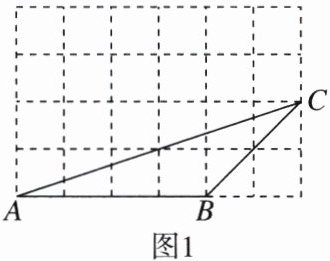
(1)∠CAB的正切值为______.
(2)分别在图1和图2中各画一个格点三角形,使得所画的三角形和△ABC相似且不全等(所画的两个三角形也不全等).



答案:
解:
(1)tan∠CAB=$\frac{2}{6}$=$\frac{1}{3}$.
(2)如图,△A'B'C'即为所求.


解:
(1)tan∠CAB=$\frac{2}{6}$=$\frac{1}{3}$.
(2)如图,△A'B'C'即为所求.


20.(8分)如图,在△ABC中,AB= AC= 4$\sqrt{5}$,$\sin C= \frac{2\sqrt{5}}{5}$.
(1)求BC的长.
(2)作以AC为直径的⊙O,使⊙O交线段AB于点D,交线段BC于点E,并求点D到BC的距离.(要求:尺规作图,保留作图痕迹,不写作法)
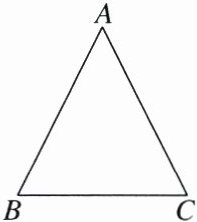
(1)求BC的长.
(2)作以AC为直径的⊙O,使⊙O交线段AB于点D,交线段BC于点E,并求点D到BC的距离.(要求:尺规作图,保留作图痕迹,不写作法)

答案:
(1)8
(2)作图略.点D到BC的距离为$\frac{16}{5}$.
(1)8
(2)作图略.点D到BC的距离为$\frac{16}{5}$.
21.(8分)将一副三角板按下图的方式摆放在一起,连结AD,求∠ADB的正切值.


答案:
解:过点A作AH⊥DB交DB的延长线于点H (图略).
设AB=k,
∵∠ACB=30°,
∴BC=$\sqrt{3}$k,
∴BD=$\frac{\sqrt{6}}{2}$k.
∵∠ABH=45°,
∴BH=AH=$\frac{\sqrt{2}}{2}$k,
DH=BD+BH=$\frac{\sqrt{6}+\sqrt{2}}{2}$k,
∴tan∠ADB=$\frac{AH}{DH}$=$\frac{\frac{\sqrt{2}}{2}k}{\frac{\sqrt{6}+\sqrt{2}}{2}k}$=$\frac{\sqrt{3}-1}{2}$.
设AB=k,
∵∠ACB=30°,
∴BC=$\sqrt{3}$k,
∴BD=$\frac{\sqrt{6}}{2}$k.
∵∠ABH=45°,
∴BH=AH=$\frac{\sqrt{2}}{2}$k,
DH=BD+BH=$\frac{\sqrt{6}+\sqrt{2}}{2}$k,
∴tan∠ADB=$\frac{AH}{DH}$=$\frac{\frac{\sqrt{2}}{2}k}{\frac{\sqrt{6}+\sqrt{2}}{2}k}$=$\frac{\sqrt{3}-1}{2}$.
查看更多完整答案,请扫码查看


