9. 在“探索函数$y= ax^2+bx+c$的系数a,b,c与图象的关系”活动中,老师给出了直角坐标系中的四个点:A(0,2),B(1,0),C(3,1),D(2,3).同学们探索了经过这四个点中的三个点的二次函数图象,发现这些图象对应的函数表达式各不相同,其中a的值最大为(

A.$ \frac{5}{2}$
B.$\frac{3}{2}$
C.$ \frac{5}{6}$
D.$ \frac{1}{2}$
A
)
A.$ \frac{5}{2}$
B.$\frac{3}{2}$
C.$ \frac{5}{6}$
D.$ \frac{1}{2}$
答案:
A
10. 已知二次函数$y= x^2-2x+m,A(x_1,y_1),B(x_2,y_2)(x_1<x_2)$是图象上两点,下列结论中正确的是(
A.若$x_1+x_2<2,$则$y_1>y_2$
B.若$x_1+x_2>2,$则$y_1>y_2$
C.若$x_1+x_2<-2,$则$y_1<y_2$
D.若$x_1+x_2>-2,$则$y_1>y_2$
A
)A.若$x_1+x_2<2,$则$y_1>y_2$
B.若$x_1+x_2>2,$则$y_1>y_2$
C.若$x_1+x_2<-2,$则$y_1<y_2$
D.若$x_1+x_2>-2,$则$y_1>y_2$
答案:
A
11. 若二次函数$y= ax^2$的图象开口向上,则a的取值范围是
$a>0$
.
答案:
$a>0$
12. 二次函数$y= x^2-2x+1$的图象与y轴的交点坐标是
$(0,1)$
.
答案:
$(0,1)$
13. 抛物线$y= -2(x+3)^2-4$有最
高
点(填“高”或“低”),此点坐标为$(-3,-4)$
.
答案:
高 $(-3,-4)$
14. 如图,已知二次函数$y= -x^2+2x$的图象,若方程$-x^2+2x= n$有实数解,则n的取值范围是

$n\leqslant1$
.
答案:
$n\leqslant1$
15. 如图,这是二次函数$y= ax^2+bx+c(a≠0)$的图象,对称轴是直线x= 1.有下列结论:$①b^2>4ac.②4a-2b+c<0.③$不等式$ax^2+bx+c>0$的解集是x≥3.5.④若$(-2,y_1),(5,y_2)$是抛物线上的两点,则$y_1<y_2.$其中正确的是
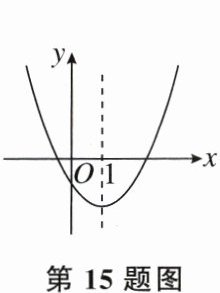
①④
.(填上所有正确结论的序号)
答案:
①④
16. 若实数a,b满足$a^2+b^2-2a= 0,$则$4a+b^2$的最大值为
8
.
答案:
8【解析】设$y = 4a + b^{2}$,则$b^{2}=y - 4a$.
$\because a^{2}+b^{2}-2a = 0$,
$\therefore a^{2}+y - 4a - 2a = 0$,
$\therefore y=-a^{2}+6a=-(a^{2}-6a + 9 - 9)=-(a - 3)^{2}+9$.
$\because b^{2}=y - 4a$,
$\therefore y - 4a\geqslant0$,即$-a^{2}+6a - 4a=-a^{2}+2a\geqslant0$,
$\therefore 0\leqslant a\leqslant2$.
$\because$当$a<3$时,$y$随$a$的增大而增大,
$\therefore$当$a = 2$时,$y$有最大值,
即$4a + b^{2}$有最大值,最大值为8.
$\because a^{2}+b^{2}-2a = 0$,
$\therefore a^{2}+y - 4a - 2a = 0$,
$\therefore y=-a^{2}+6a=-(a^{2}-6a + 9 - 9)=-(a - 3)^{2}+9$.
$\because b^{2}=y - 4a$,
$\therefore y - 4a\geqslant0$,即$-a^{2}+6a - 4a=-a^{2}+2a\geqslant0$,
$\therefore 0\leqslant a\leqslant2$.
$\because$当$a<3$时,$y$随$a$的增大而增大,
$\therefore$当$a = 2$时,$y$有最大值,
即$4a + b^{2}$有最大值,最大值为8.
17. (8分)已知函数$y= (k^2-k)x^2+kx+k+1(k$为常数).
(1)若这个函数是一次函数,求k的值.
(2)若这个函数是二次函数,则k的值满足什么条件?
(1)若这个函数是一次函数,求k的值.
(2)若这个函数是二次函数,则k的值满足什么条件?
答案:
解:
(1)若这个函数是一次函数,
则$k^{2}-k = 0$且$k\neq0$,
解得$k = 1$.
(2)若这个函数是二次函数,
则$k^{2}-k\neq0$,
解得$k\neq0$且$k\neq1$.
(1)若这个函数是一次函数,
则$k^{2}-k = 0$且$k\neq0$,
解得$k = 1$.
(2)若这个函数是二次函数,
则$k^{2}-k\neq0$,
解得$k\neq0$且$k\neq1$.
查看更多完整答案,请扫码查看


