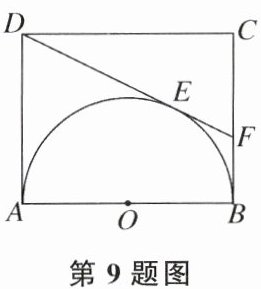
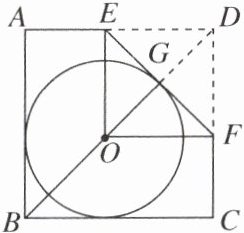
9. 在矩形ABCD中,$AB= 4$,$AD= 3$,以AB为直径在矩形内作半圆. DE切$\odot O$于点E(如图),则$\tan\angle CDF$的值为(
A.$\frac{3}{4}$
B.$\frac{5}{12}$
C.$\frac{5}{13}$
D.$\frac{4}{9}$
B
)
A.$\frac{3}{4}$
B.$\frac{5}{12}$
C.$\frac{5}{13}$
D.$\frac{4}{9}$
答案:
B
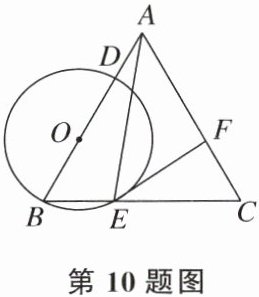
10. 如图,在等边三角形ABC中,点O在边AB上,$\odot O$过点B且分别与边AB,BC相交于点D,E,F是AC上的点,则下列说法中错误的是(
A.若$EF\perp AC$,则EF是$\odot O$的切线
B.若EF是$\odot O$的切线,则$EF\perp AC$
C.若$BE= EC$,则AC是$\odot O$的切线
D.若$BE= \frac{\sqrt{3}}{2}EC$,则AC是$\odot O$的切线
C
)
A.若$EF\perp AC$,则EF是$\odot O$的切线
B.若EF是$\odot O$的切线,则$EF\perp AC$
C.若$BE= EC$,则AC是$\odot O$的切线
D.若$BE= \frac{\sqrt{3}}{2}EC$,则AC是$\odot O$的切线
答案:
C
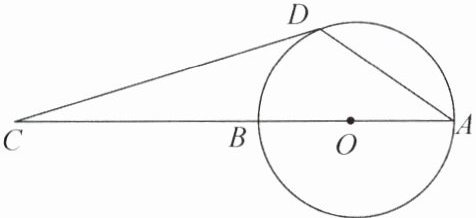
11. 如图,AB是$\odot O$的直径,点C在AB的延长线上,CD与$\odot O$相切于点D,若$\angle C= 20°$,则$\angle CAD= $
35
°.
答案:
35
12. 已知$\odot O的半径是一元二次方程x^2-2x-3= 0$的一个根,圆心O到直线l的距离为4,则直线l与$\odot O$有
0
个交点.
答案:
0
13. 如图,以点O为圆心的两个圆中,大圆的弦AB切小圆于点C,OA交小圆于点D,若$OD= 2$,$\tan\angle OAB= \frac{1}{2}$,则AB的长是

8
.
答案:
8
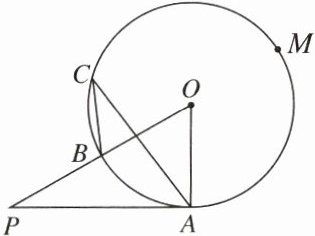
14. 如图,PA切$\odot O$于点A,PO交$\odot O$于点B,点C是$\widehat{AMB}$上一点,连结AC,BC,如果$\angle P= \angle C$,$\odot O$的半径为1,则$\widehat{AB}$的长为
$\frac{π}{3}$
.
答案:
$\frac{π}{3}$
15. 如图,O是正方形ABCD的对角线BD上一点,$\odot O$与边AB,BC都相切,点E,F分别在AD,DC上,现将$\triangle DEF$沿着EF对折,折痕EF与$\odot O$相切,此时点D恰好落在圆心O处. 若$DE= 2$,则正方形ABCD的边长是
2+$\sqrt{2}$
.
答案:
2+$\sqrt{2}$
查看更多完整答案,请扫码查看


