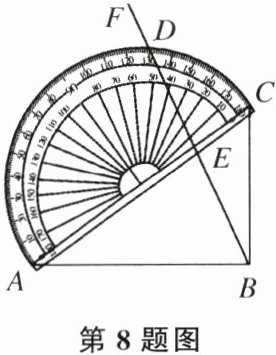
8. 如图,在Rt△ABC中,∠CAB= 36°,斜边AC与量角器的直径重合(点A的刻度为0),将射线BF绕着点B转动,与量角器的外圆弧交于点D,与AC交于点E,若△ABE是等腰三角形,则点D在量角器上对应的刻度为( )
A.72°
B.144°
C.36°或72°
D.72°或144°

A.72°
B.144°
C.36°或72°
D.72°或144°
答案:
A 【解析】连结 OE,OD.
∵AC 为⊙O 的直径,
∴∠AEC=90°.
∵AB=AC,
∴BE=CE,
即 E 是 BC 的中点.
∵O 是 AC 的中点,
∴OE 是△ABC 的中位线,
∴OE//AB,
∴$S_{\triangle AOD}=S_{\triangle AED}$,
∴$S_{阴影}=S_{扇形 AOD}$.
∵∠AEC=90°,
∴∠AEB=90°,
∵∠BED=45°,
∴∠AED=45°,
∴∠AOD=90°,
∴$S_{扇形 AOD}=\frac{90\pi×1^{2}}{360}=\frac{\pi}{4}$,
∴$S_{阴影}=\frac{\pi}{4}$.

A 【解析】连结 OE,OD.
∵AC 为⊙O 的直径,
∴∠AEC=90°.
∵AB=AC,
∴BE=CE,
即 E 是 BC 的中点.
∵O 是 AC 的中点,
∴OE 是△ABC 的中位线,
∴OE//AB,
∴$S_{\triangle AOD}=S_{\triangle AED}$,
∴$S_{阴影}=S_{扇形 AOD}$.
∵∠AEC=90°,
∴∠AEB=90°,
∵∠BED=45°,
∴∠AED=45°,
∴∠AOD=90°,
∴$S_{扇形 AOD}=\frac{90\pi×1^{2}}{360}=\frac{\pi}{4}$,
∴$S_{阴影}=\frac{\pi}{4}$.

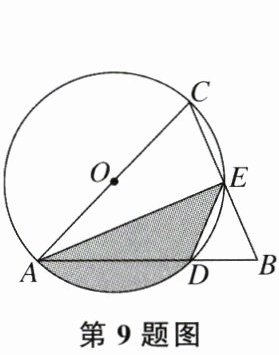
9. 如图,在△ABC中,AB= AC,以AC为直径的⊙O与AB,BC分别交于点D,E,连结AE,DE,若∠BED= 45°,AB= 2,则阴影部分的面积为( )
A.π/4
B.π/3
C.2π/3
D.π

A.π/4
B.π/3
C.2π/3
D.π
答案:
C 【解析】如图,过点 O 作 OF⊥CD 于点 F,OG⊥AB 于点 G,
连结 OB,OD,OE.
则 DF=CF,AG=BG=$\frac{1}{2}$AB =3,
∴EG=AG - AE=2.
在 Rt△BOG 中,OG=$\sqrt{OB^{2}-BG^{2}}=\sqrt{13 - 9}=2$,
∴EG=OG,
∴△EOG 是等腰直角三角形,
∴∠OEG=45°,OE=$\sqrt{2}$OG=$2\sqrt{2}$.
∵∠DEB=75°,
∴∠OEF=30°,
∴OF=$\frac{1}{2}$OE=$\sqrt{2}$
在 Rt△ODF 中,DF=$\sqrt{OD^{2}-OF^{2}}=\sqrt{13 - 2}=\sqrt{11}$,
∴CD=2DF=$2\sqrt{11}$

C 【解析】如图,过点 O 作 OF⊥CD 于点 F,OG⊥AB 于点 G,
连结 OB,OD,OE.
则 DF=CF,AG=BG=$\frac{1}{2}$AB =3,
∴EG=AG - AE=2.
在 Rt△BOG 中,OG=$\sqrt{OB^{2}-BG^{2}}=\sqrt{13 - 9}=2$,
∴EG=OG,
∴△EOG 是等腰直角三角形,
∴∠OEG=45°,OE=$\sqrt{2}$OG=$2\sqrt{2}$.
∵∠DEB=75°,
∴∠OEF=30°,
∴OF=$\frac{1}{2}$OE=$\sqrt{2}$
在 Rt△ODF 中,DF=$\sqrt{OD^{2}-OF^{2}}=\sqrt{13 - 2}=\sqrt{11}$,
∴CD=2DF=$2\sqrt{11}$

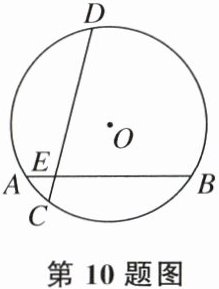
10. 如图,在半径为√13的⊙O中,弦AB与CD相交于点E,∠DEB= 75°,AB= 6,AE= 1,则CD的长是(
A.2√6
B.2√10
C.2√11
D.4√3
C
)
A.2√6
B.2√10
C.2√11
D.4√3
答案:
C
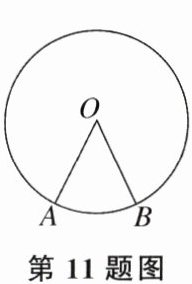
11. 如图,若圆心角∠AOB= 40°,则弧AB的度数是
40
度.
答案:
40
12. 已知△ABC的三边长分别是6,8,10,则△ABC外接圆的直径是
10
.
答案:
10
13. 制作弯形管道时,需要先按中心线计算“展直长度”再下料.试计算如图所示的管道的展直长度,即$\overset{\frown}{AB}$的长为

20π
mm.
答案:
20π
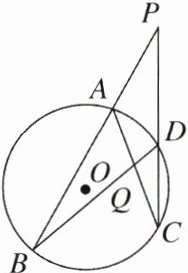
14. 如图,A,B,C,D是⊙O上的四个点,BA,CD的延长线相交于点P,AC,BD相交于点Q.若∠P= 30°,∠AQD= 72°,则∠B的度数是
21
°.
答案:
21
15. F是正五边形ABCDE的边DE的中点,连结BF并延长与CD的延长线交于点G,则∠BGC的度数为

18°
.
答案:
18°
16. 如图,AB是⊙O的直径,C是⊙O上一点,D是弧BC的中点,DE⊥AB于点E,交BC于点F,已知AC= 2,⊙O的半径为2,则BF的长为______.


答案:
$\frac{2\sqrt{3}}{3}$ 【解析】延长 DE 交圆 O 于点 G,连结 BD,OD,如图所示.
∵D 是弧 BC 的中点,
∴$\overset{\frown}{CD}=\overset{\frown}{DB}$.
又
∵DE⊥AB,
∴$\overset{\frown}{DB}=\overset{\frown}{BG}$,
∴$\overset{\frown}{CD}=\overset{\frown}{BG}$,
∴∠DBC=∠BDF,
∴DF=BF.
∵AB 为⊙O 的直径,⊙O 的半径为 2,
∴AB=4,
∴∠ACB=90°,OB=OD=2,
∴BC=$\sqrt{4^{2}-2^{2}}=2\sqrt{3}$
∵$\overset{\frown}{CD}=\overset{\frown}{DB}=\overset{\frown}{BG}$,
∴$\overset{\frown}{BC}=\overset{\frown}{DG}$,
∴BC=DG=2DE.
即 DE=$\frac{1}{2}$BC=$\sqrt{3}$
∵DE⊥AB,
∴OE=$\sqrt{2^{2}-(\sqrt{3})^{2}}=1$,
∴BE=OB - OE=1.
设 DF=BF=a,则 EF=$\sqrt{3}-a$,
在 Rt△BEF 中,由勾股定理得$1^{2}+(\sqrt{3}-a)^{2}=a^{2}$,
解得$a=\frac{2\sqrt{3}}{3}$,
∴BF=DF=$\frac{2\sqrt{3}}{3}$.

$\frac{2\sqrt{3}}{3}$ 【解析】延长 DE 交圆 O 于点 G,连结 BD,OD,如图所示.
∵D 是弧 BC 的中点,
∴$\overset{\frown}{CD}=\overset{\frown}{DB}$.
又
∵DE⊥AB,
∴$\overset{\frown}{DB}=\overset{\frown}{BG}$,
∴$\overset{\frown}{CD}=\overset{\frown}{BG}$,
∴∠DBC=∠BDF,
∴DF=BF.
∵AB 为⊙O 的直径,⊙O 的半径为 2,
∴AB=4,
∴∠ACB=90°,OB=OD=2,
∴BC=$\sqrt{4^{2}-2^{2}}=2\sqrt{3}$
∵$\overset{\frown}{CD}=\overset{\frown}{DB}=\overset{\frown}{BG}$,
∴$\overset{\frown}{BC}=\overset{\frown}{DG}$,
∴BC=DG=2DE.
即 DE=$\frac{1}{2}$BC=$\sqrt{3}$
∵DE⊥AB,
∴OE=$\sqrt{2^{2}-(\sqrt{3})^{2}}=1$,
∴BE=OB - OE=1.
设 DF=BF=a,则 EF=$\sqrt{3}-a$,
在 Rt△BEF 中,由勾股定理得$1^{2}+(\sqrt{3}-a)^{2}=a^{2}$,
解得$a=\frac{2\sqrt{3}}{3}$,
∴BF=DF=$\frac{2\sqrt{3}}{3}$.

查看更多完整答案,请扫码查看


