搜索
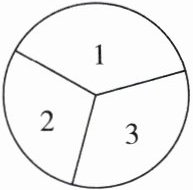
22. (10分)将6个球分别放入标有1,2,3,4,5,6这6个号码的盒子中.如图,将一个圆形转盘平均分成3份,分别标上数字1,2,3.现转动转盘两次,两次转得的数字之和是几,就从几号盒子中摸出一个球(如:第一次转得的数字为2,第二次转得的数字为3,则和为5,就从5号盒子中摸球).
(1)求从6号盒子中摸球的概率.
(2)通过计算,判断从几号盒子中摸球的概率最大.
(1)求从6号盒子中摸球的概率.
(2)通过计算,判断从几号盒子中摸球的概率最大.
答案：
解:
(1)画树状图如下:
共有9种等可能的结果，其中和为6的结果有1种,
∴从6号盒子中摸球的概率为$\frac{1}{9}$.
(2)由
(1)可知,共有9种等可能的结果，其中从2号盒子中摸球的结果有1种,从6号盒子中摸球的结果有1种,从3号盒子中摸球的结果有2种,从5号盒子中摸球的结果有2种,从1号盒子中摸球的结果有0种,从4号盒子中摸球的结果有3种,是最多的,
∴从2号盒子中摸球的概率 = 从6号盒子中摸球的概率 = $\frac{1}{9}$,从3号盒子中摸球的概率 = 从5号盒子中摸球的概率 = $\frac{2}{9}$,从1号盒子中摸球的概率为0,从4号盒子中摸球的概率为$\frac{3}{9}$=$\frac{1}{3}$,
∵$\frac{1}{3}$＞$\frac{2}{9}$＞$\frac{1}{9}$＞0,
∴从4号盒子中摸球的概率最大.
解:
(1)画树状图如下:
共有9种等可能的结果，其中和为6的结果有1种,∴从6号盒子中摸球的概率为$\frac{1}{9}$.
(2)由
(1)可知,共有9种等可能的结果，其中从2号盒子中摸球的结果有1种,从6号盒子中摸球的结果有1种,从3号盒子中摸球的结果有2种,从5号盒子中摸球的结果有2种,从1号盒子中摸球的结果有0种,从4号盒子中摸球的结果有3种,是最多的,
∴从2号盒子中摸球的概率 = 从6号盒子中摸球的概率 = $\frac{1}{9}$,从3号盒子中摸球的概率 = 从5号盒子中摸球的概率 = $\frac{2}{9}$,从1号盒子中摸球的概率为0,从4号盒子中摸球的概率为$\frac{3}{9}$=$\frac{1}{3}$,
∵$\frac{1}{3}$＞$\frac{2}{9}$＞$\frac{1}{9}$＞0,
∴从4号盒子中摸球的概率最大.
23. (10分)刘雨泽和黎昕两名同学玩抽数字游戏.五张卡片上分别写有2,4,6,8,$x$这五个数字,其中两张卡片上的数字是相同的,从中随机抽出一张,已知$P$(抽到数字4的卡片)$=\frac{2}{5}$.
(1)求这五张卡片上的数字的众数.
(2)若刘雨泽已抽走一张数字2的卡片,黎昕准备从剩余4张卡片中抽出一张.
①所剩的4张卡片上数字的中位数与原来5张卡片上数字的中位数是否相同？并简要说明理由.
②黎昕先随机抽出一张卡片后放回,之后又随机抽出一张,用列表法或画树状图法求黎昕两次都抽到数字4的概率.
(1)求这五张卡片上的数字的众数.
(2)若刘雨泽已抽走一张数字2的卡片,黎昕准备从剩余4张卡片中抽出一张.
①所剩的4张卡片上数字的中位数与原来5张卡片上数字的中位数是否相同？并简要说明理由.
②黎昕先随机抽出一张卡片后放回,之后又随机抽出一张,用列表法或画树状图法求黎昕两次都抽到数字4的概率.
答案：
解:
(1)
∵2,4,6,8,x这五个数字中,P(抽到数字4的卡片)=$\frac{2}{5}$,则数字4的卡片有2张,即x = 4,
∴五个数字分别为2,4,4,6,8,则众数为4.
(2)①不同,理由:原来5张卡片上数字的中位数为4,抽走数字2后,所剩的4张卡片上的数字为4,4,6,8,中位数为5,所以不同. ②根据题意画树状图如下:
可得共有16种等可能的结果，其中两次都抽到数字4的情况有4种,则黎昕两次都抽到数字4的概率为$\frac{4}{16}$=$\frac{1}{4}$.
解:
(1)
∵2,4,6,8,x这五个数字中,P(抽到数字4的卡片)=$\frac{2}{5}$,则数字4的卡片有2张,即x = 4,
∴五个数字分别为2,4,4,6,8,则众数为4.
(2)①不同,理由:原来5张卡片上数字的中位数为4,抽走数字2后,所剩的4张卡片上的数字为4,4,6,8,中位数为5,所以不同. ②根据题意画树状图如下:
可得共有16种等可能的结果，其中两次都抽到数字4的情况有4种,则黎昕两次都抽到数字4的概率为$\frac{4}{16}$=$\frac{1}{4}$. 24. (12分)在一个不透明的口袋里装有分别标有数字$-3,-1,0,2$的四个小球,除数字不同外,小球没有任何区别,每次试验先搅拌均匀.
(1)从中任取一球,求抽取的数字为正数的概率.
(2)从中任取一球,将球上的数字记为$a$,求关于$x的一元二次方程ax^2-2ax+a+3= 0$有实数根的概率.
(3)从中抽取一球,将球上的数字作为点的横坐标,记为$x$(不放回);再任取一球,将球上的数字作为点的纵坐标,记为$y$,试用画树状图或列表法表示出点$(x,y)$所有可能出现的结果,并求点$(x,y)$落在第二象限内的概率.
(1)从中任取一球,求抽取的数字为正数的概率.
(2)从中任取一球,将球上的数字记为$a$,求关于$x的一元二次方程ax^2-2ax+a+3= 0$有实数根的概率.
(3)从中抽取一球,将球上的数字作为点的横坐标,记为$x$(不放回);再任取一球,将球上的数字作为点的纵坐标,记为$y$,试用画树状图或列表法表示出点$(x,y)$所有可能出现的结果,并求点$(x,y)$落在第二象限内的概率.
答案：
解:
(1)由题意,得抽取的数字为正数的情况有1种,故抽取的数字为正数的概率为$\frac{1}{4}$.
(2)
∵一元二次方程$ax^{2}-2ax+a + 3 = 0$有实数根,
∴$4a^{2}-4a(a + 3)=-12a\geq 0$, 且$a\neq 0$,解得$a ＜ 0$,
∴方程$ax^{2}-2ax+a + 3 = 0$有实数根的概率为$\frac{1}{2}$.
(3)列表: x y −3 −1 0 2 −3 (−1,−3) (0,−3) (2,−3) −1 (−3,−1) (0,−1) (2,−1) 0 (−3,0) (−1,0) (2,0) 2 (−3,2) (−1,2) (0,2) 所有等可能出现的结果有12种,其中点$(x,y)$落在第二象限内的结果有2种,则所求概率为$\frac{2}{12}$=$\frac{1}{6}$.
(1)由题意,得抽取的数字为正数的情况有1种,故抽取的数字为正数的概率为$\frac{1}{4}$.
(2)
∵一元二次方程$ax^{2}-2ax+a + 3 = 0$有实数根,
∴$4a^{2}-4a(a + 3)=-12a\geq 0$, 且$a\neq 0$,解得$a ＜ 0$,
∴方程$ax^{2}-2ax+a + 3 = 0$有实数根的概率为$\frac{1}{2}$.
(3)列表: x y −3 −1 0 2 −3 (−1,−3) (0,−3) (2,−3) −1 (−3,−1) (0,−1) (2,−1) 0 (−3,0) (−1,0) (2,0) 2 (−3,2) (−1,2) (0,2) 所有等可能出现的结果有12种,其中点$(x,y)$落在第二象限内的结果有2种,则所求概率为$\frac{2}{12}$=$\frac{1}{6}$.
查看更多完整答案，请扫码查看
