22. (10分)如图,利用一面墙(墙的长度不超过45 m),用79 m长的篱笆围成一个矩形场地,并且与墙平行的边留有1 m宽建造一扇门方便出入(用其他材料).设AB= x m,矩形ABCD的面积为$y m^2.$
(1)请求出y与x之间的函数关系式,并写出x的取值范围.
(2)怎样围才能使矩形场地的面积为$750 m^2?$
(3)当x为何值时,矩形场地的面积最大?最大值为多少?

(1)请求出y与x之间的函数关系式,并写出x的取值范围.
(2)怎样围才能使矩形场地的面积为$750 m^2?$
(3)当x为何值时,矩形场地的面积最大?最大值为多少?

答案:
解:
(1)由题意得,$AD = BC = \frac{1}{2}(79 - x + 1)=(40 - \frac{1}{2}x)m$,
则$y = x(40 - \frac{1}{2}x)=-\frac{1}{2}x^{2}+40x(0<x≤45)$,故$y$与$x$之间的函数关系式为$y = -\frac{1}{2}x^{2}+40x(0<x≤45)$。
(2)令$y = -\frac{1}{2}x^{2}+40x = 750$,
解得$x = 50$(舍去)或$x = 30$,
即当$AB = 30m$时,矩形场地的面积为$750m^{2}$。
(3)
∵$y = -\frac{1}{2}x^{2}+40x = -\frac{1}{2}(x - 40)^{2}+800≤800$,
∴当$x = 40$时,矩形场地的面积最大,最大值为$800m^{2}$。
(1)由题意得,$AD = BC = \frac{1}{2}(79 - x + 1)=(40 - \frac{1}{2}x)m$,
则$y = x(40 - \frac{1}{2}x)=-\frac{1}{2}x^{2}+40x(0<x≤45)$,故$y$与$x$之间的函数关系式为$y = -\frac{1}{2}x^{2}+40x(0<x≤45)$。
(2)令$y = -\frac{1}{2}x^{2}+40x = 750$,
解得$x = 50$(舍去)或$x = 30$,
即当$AB = 30m$时,矩形场地的面积为$750m^{2}$。
(3)
∵$y = -\frac{1}{2}x^{2}+40x = -\frac{1}{2}(x - 40)^{2}+800≤800$,
∴当$x = 40$时,矩形场地的面积最大,最大值为$800m^{2}$。
23. (10分)在平面直角坐标系中,已知二次函数$y= ax^2+(a+2)x+1$(a≠0,a是常数).
(1)若该函数的图象经过点(1,1),求该二次函数图象的顶点坐标.
(2)若点(m,y1),(n,y2)是该二次函数的图象上两个不同的点,则:
①当m+n= -2时,如果恒有y1= y2,求此二次函数的最值.
②当a>2且n>m≥-$\frac{1}{2}$时,求证:y2>y1.
(1)若该函数的图象经过点(1,1),求该二次函数图象的顶点坐标.
(2)若点(m,y1),(n,y2)是该二次函数的图象上两个不同的点,则:
①当m+n= -2时,如果恒有y1= y2,求此二次函数的最值.
②当a>2且n>m≥-$\frac{1}{2}$时,求证:y2>y1.
答案:
解:
(1)
∵函数的图象经过点$(1,1)$,
∴将点的坐标代入$y = ax^{2}+(a + 2)x + 1$,
解得$a = - 1$,
∴$y = - x^{2}+(-1 + 2)x + 1=-x^{2}+x + 1=-(x - \frac{1}{2})^{2}+\frac{5}{4}$,
∴二次函数图象的顶点坐标为$(\frac{1}{2},\frac{5}{4})$。
(2)①
∵当$m + n = - 2$时,恒有$y_1 = y_2$,
∴对称轴方程为$x = \frac{-2}{2} = - 1$,
∴$-\frac{a + 2}{2a} = - 1$,解得$a = 2$,
∴二次函数的表达式为$y = 2x^{2}+4x + 1=2(x + 1)^{2}-1$,
∴当$x = - 1$时,此二次函数的最值为$-1$。
②证明:对称轴为直线$x = -\frac{a + 2}{2a}=-\frac{1}{2}-\frac{1}{a}$。
∵$a>2$,
∴$x = -\frac{1}{2}-\frac{1}{a}<-\frac{1}{2}$,二次函数图象开口向上,当$x>-\frac{1}{2}-\frac{1}{a}$时,$y$随$x$的增大而增大。
∵$n>m≥-\frac{1}{2}$,
∴$y_2>y_1$。
(1)
∵函数的图象经过点$(1,1)$,
∴将点的坐标代入$y = ax^{2}+(a + 2)x + 1$,
解得$a = - 1$,
∴$y = - x^{2}+(-1 + 2)x + 1=-x^{2}+x + 1=-(x - \frac{1}{2})^{2}+\frac{5}{4}$,
∴二次函数图象的顶点坐标为$(\frac{1}{2},\frac{5}{4})$。
(2)①
∵当$m + n = - 2$时,恒有$y_1 = y_2$,
∴对称轴方程为$x = \frac{-2}{2} = - 1$,
∴$-\frac{a + 2}{2a} = - 1$,解得$a = 2$,
∴二次函数的表达式为$y = 2x^{2}+4x + 1=2(x + 1)^{2}-1$,
∴当$x = - 1$时,此二次函数的最值为$-1$。
②证明:对称轴为直线$x = -\frac{a + 2}{2a}=-\frac{1}{2}-\frac{1}{a}$。
∵$a>2$,
∴$x = -\frac{1}{2}-\frac{1}{a}<-\frac{1}{2}$,二次函数图象开口向上,当$x>-\frac{1}{2}-\frac{1}{a}$时,$y$随$x$的增大而增大。
∵$n>m≥-\frac{1}{2}$,
∴$y_2>y_1$。
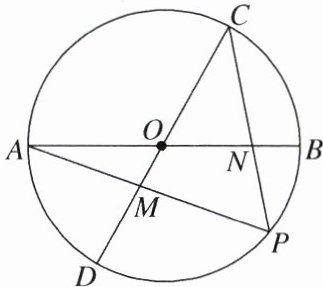
24. (12分)如图,⊙O的半径为1,直径AB,CD的夹角∠AOD= 60°,P是$\widehat{BD}$上一点,连结PA,PC分别交CD,AB于点M,N.
(1)若PC⊥AB,求证:PA⊥CD.
(2)当点P在$\widehat{BD}$上运动时,
①猜想:线段AM与CN有怎样的数量关系,并给出证明.
②求证:PA+PC= $\frac{3}{AM}$.
(1)若PC⊥AB,求证:PA⊥CD.
(2)当点P在$\widehat{BD}$上运动时,
①猜想:线段AM与CN有怎样的数量关系,并给出证明.
②求证:PA+PC= $\frac{3}{AM}$.

答案:
解:
(1)证明:
∵$∠AOD = ∠BOC = 60°$,$PC⊥AB$
∴$\widehat{BC}=\widehat{BP}=60°$,
∴$∠BAP = 30°$,
∴$∠AMO = 180° - ∠MAO - ∠AOM = 180° - 30° - 60° = 90°$,
∴$PA⊥CD$。
(2)①$AM = CN$。证明如下:
连结AD,如图。
∵$OA = OD$,$∠AOD = 60°$,
∴$△OAD$是等边三角形,
∴$∠D = 60°$,$OA = AD = OD$。
∵$OC = OD$,
∴$AD = OC$。
又
∵$∠DAP = ∠DCP$,$∠D = ∠BOC = 60°$,
∴$△ADM\cong△CON(ASA)$,
∴$AM = CN$。
②证明:
∵$\odot O$的半径为1,
∴$OA = OB = OC = OD = 1$。
∵$∠P = ∠D = 60°$,$∠AOD = 60°$,
∴$∠P = ∠AOD$。
又
∵$∠BAP = ∠BAP$,
∴$△AOM\sim△APN$,
∴$\frac{OA}{PA}=\frac{AM}{AN}$,
∴$\frac{1}{PA}=\frac{AM}{AN}$,
即$PA=\frac{AN}{AM}$。
∵$∠BOC = ∠CPM = 60°$,$∠C = ∠C$,
∴$△CON\sim△CPM$,
∴$\frac{CN}{CM}=\frac{OC}{PC}$,
∴$PC=\frac{CM}{CN}$。
由①知$△ADM\cong△CON$,
∴$AM = CN$,$DM = ON$。
又
∵$DM + OM = OD = 1$,
∴$PA + PC=\frac{AN}{AM}+\frac{CM}{CN}=\frac{1 + ON + 1 + OM}{AM}=\frac{1 + DM + 1 + OM}{AM}=\frac{3}{AM}$。
(1)证明:
∵$∠AOD = ∠BOC = 60°$,$PC⊥AB$
∴$\widehat{BC}=\widehat{BP}=60°$,
∴$∠BAP = 30°$,
∴$∠AMO = 180° - ∠MAO - ∠AOM = 180° - 30° - 60° = 90°$,
∴$PA⊥CD$。
(2)①$AM = CN$。证明如下:
连结AD,如图。
∵$OA = OD$,$∠AOD = 60°$,
∴$△OAD$是等边三角形,
∴$∠D = 60°$,$OA = AD = OD$。
∵$OC = OD$,
∴$AD = OC$。
又
∵$∠DAP = ∠DCP$,$∠D = ∠BOC = 60°$,
∴$△ADM\cong△CON(ASA)$,
∴$AM = CN$。
②证明:
∵$\odot O$的半径为1,
∴$OA = OB = OC = OD = 1$。
∵$∠P = ∠D = 60°$,$∠AOD = 60°$,
∴$∠P = ∠AOD$。
又
∵$∠BAP = ∠BAP$,
∴$△AOM\sim△APN$,
∴$\frac{OA}{PA}=\frac{AM}{AN}$,
∴$\frac{1}{PA}=\frac{AM}{AN}$,
即$PA=\frac{AN}{AM}$。
∵$∠BOC = ∠CPM = 60°$,$∠C = ∠C$,
∴$△CON\sim△CPM$,
∴$\frac{CN}{CM}=\frac{OC}{PC}$,
∴$PC=\frac{CM}{CN}$。
由①知$△ADM\cong△CON$,
∴$AM = CN$,$DM = ON$。
又
∵$DM + OM = OD = 1$,
∴$PA + PC=\frac{AN}{AM}+\frac{CM}{CN}=\frac{1 + ON + 1 + OM}{AM}=\frac{1 + DM + 1 + OM}{AM}=\frac{3}{AM}$。
查看更多完整答案,请扫码查看


