22.(10分)如图,在四边形ABCD中,以AB为直径的半圆O经过点C,AC与BD相交于点E,$CD^2= CE \cdot CA$,分别延长AB,DC相交于点P,$PB= BO$,$CD= 2\sqrt{2}$.
(1)求证:AC平分$\angle DAB$.
(2)求线段BO的长.
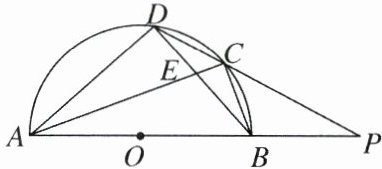
(1)求证:AC平分$\angle DAB$.
(2)求线段BO的长.

答案:
解:
(1)证明:
∵$CD^{2}=CE\cdot CA$,
∴$\frac{CD}{CE}=\frac{CA}{CD}$.
∵∠ACD=∠DCE,
∴△ACD∽△DCE,
∴∠CAD=∠CDE.
∵∠CDE=∠CAB,
∴∠CAD=∠CAB,
∴AC平分∠DAB.
(2)由
(1)知,∠CAD=∠CAB,
∴$\overset{\frown}{CD}=\overset{\frown}{BC}$,
∴BC=CD=$2\sqrt{2}$.
∵AB是⊙O的直径,
∴∠ADB=90°,即AD⊥BD.
如图,连结OC,
易得OC⊥BD,
∴AD//OC,
∴∠COP=∠DAB.
设OB=OC=r,则BP=r,OP=2r.
∵四边形ABCD是内接四边形,
∴∠PCB=∠DAB=∠COP.
又
∵∠CPB=∠OPC,
∴△CPB∽△OPC,
∴$\frac{PB}{PC}=\frac{BC}{OC}=\frac{PC}{OP}$,即$\frac{r}{PC}=\frac{2\sqrt{2}}{r}=\frac{PC}{2r}$,
解得PC=$4\sqrt{2}$,r=4,
∴OB的长为4.

解:
(1)证明:
∵$CD^{2}=CE\cdot CA$,
∴$\frac{CD}{CE}=\frac{CA}{CD}$.
∵∠ACD=∠DCE,
∴△ACD∽△DCE,
∴∠CAD=∠CDE.
∵∠CDE=∠CAB,
∴∠CAD=∠CAB,
∴AC平分∠DAB.
(2)由
(1)知,∠CAD=∠CAB,
∴$\overset{\frown}{CD}=\overset{\frown}{BC}$,
∴BC=CD=$2\sqrt{2}$.
∵AB是⊙O的直径,
∴∠ADB=90°,即AD⊥BD.
如图,连结OC,
易得OC⊥BD,
∴AD//OC,
∴∠COP=∠DAB.
设OB=OC=r,则BP=r,OP=2r.
∵四边形ABCD是内接四边形,
∴∠PCB=∠DAB=∠COP.
又
∵∠CPB=∠OPC,
∴△CPB∽△OPC,
∴$\frac{PB}{PC}=\frac{BC}{OC}=\frac{PC}{OP}$,即$\frac{r}{PC}=\frac{2\sqrt{2}}{r}=\frac{PC}{2r}$,
解得PC=$4\sqrt{2}$,r=4,
∴OB的长为4.

23.(10分)如图,在矩形ABCD中,点E,F分别在CD,AD上,连结AE,BF,$AE \perp BF且AE= BF$.
(1)求证:$AB= AD$.
(2)连结EF,BE,线段FD是线段AD与AF的比例中项.
①若$AD= 4$,求线段FD的长.
②求证:$\triangle DEF \backsim \triangle CEB$.

(1)求证:$AB= AD$.
(2)连结EF,BE,线段FD是线段AD与AF的比例中项.
①若$AD= 4$,求线段FD的长.
②求证:$\triangle DEF \backsim \triangle CEB$.

答案:
解:
(1)证明:
∵四边形ABCD是矩形,
∴∠BAD=∠ADE=90°,
∴∠ABF+∠AFB=90°.
∵AE⊥BF,
∴∠DAE+∠AFB=90°,
∴∠ABF=∠DAE.在△ABF和△DAE中,
$\begin{cases}∠ABF=∠DAE, \\∠BAF=∠ADE=90°, \\BF=AE,\end{cases}$
∴△ABF≌△DAE(AAS),
∴AB=AD.
(2)①
∵线段DF是线段AD与AF的比例中项,
∴$DF^{2}=AF\cdot AD$.
∵AD=4,
∴$DF^{2}=(4-DF)×4$,
∴DF=-2+$2\sqrt{5}$(负值舍去).
②证明:由
(1)可知,△ABF≌△DAE,AB=AD,
∴AF=DE,
∴DF=CE.
∵线段DF是线段AD与AF的比例中项,
∴$DF^{2}=AF\cdot AD$,
∴$\frac{DF}{AF}=\frac{DE}{DF}$.
∵∠FDE=∠BCE=90°,
∴△DEF∽△CEB.
(1)证明:
∵四边形ABCD是矩形,
∴∠BAD=∠ADE=90°,
∴∠ABF+∠AFB=90°.
∵AE⊥BF,
∴∠DAE+∠AFB=90°,
∴∠ABF=∠DAE.在△ABF和△DAE中,
$\begin{cases}∠ABF=∠DAE, \\∠BAF=∠ADE=90°, \\BF=AE,\end{cases}$
∴△ABF≌△DAE(AAS),
∴AB=AD.
(2)①
∵线段DF是线段AD与AF的比例中项,
∴$DF^{2}=AF\cdot AD$.
∵AD=4,
∴$DF^{2}=(4-DF)×4$,
∴DF=-2+$2\sqrt{5}$(负值舍去).
②证明:由
(1)可知,△ABF≌△DAE,AB=AD,
∴AF=DE,
∴DF=CE.
∵线段DF是线段AD与AF的比例中项,
∴$DF^{2}=AF\cdot AD$,
∴$\frac{DF}{AF}=\frac{DE}{DF}$.
∵∠FDE=∠BCE=90°,
∴△DEF∽△CEB.
24.(12分)如图,在$\triangle ABC$中,$AB= 4$,D是AB上一点(不与点A,B重合),$DE // BC$,交AC于点E. 设$\triangle ABC$的面积为S,$\triangle DEC的面积为S'$.
(1)当D是AB的中点时,求$\frac{S'}{S}$的值.
(2)设$AD= x$,$\frac{S'}{S}= y$,求y与x的函数表达式,并写出自变量x的取值范围.
(3)根据y的范围,求$S-4S'$的最小值.

(1)当D是AB的中点时,求$\frac{S'}{S}$的值.
(2)设$AD= x$,$\frac{S'}{S}= y$,求y与x的函数表达式,并写出自变量x的取值范围.
(3)根据y的范围,求$S-4S'$的最小值.

答案:
解:
(1)
∵D为AB的中点,
∴AB=2AD.
∵DE//BC,
∴AE=EC.
∵△ADE的边AE上的高和△CED的边CE上的高相等,
∴$S_{\triangle ADE}=S_{\triangle CDE}=S'$.
∵DE//BC,
∴△ADE∽△ABC,
∴$\frac{S_{\triangle ADE}}{S_{\triangle ABC}}=(\frac{AD}{AB})^{2}=\frac{1}{4}$,
∴$\frac{S'}{S}=\frac{1}{4}$.
(2)
∵AB=4,AD=x,
∴$\frac{S_{\triangle ADE}}{S_{\triangle ABC}}=\frac{x^{2}}{16}$①
∵DE//BC,
∴△ADE∽△ABC,
∴$\frac{AD}{AB}=\frac{AE}{AC}$.
∵AB=4,AD=x,
∴$\frac{AE}{AC}=\frac{x}{4}$,
∴$\frac{AE}{CE}=\frac{x}{4-x}$.
∵△ADE的边AE上的高和△CED的边CE上的高相等,
∴$\frac{S_{\triangle ADE}}{S_{\triangle CDE}}=\frac{AE}{CE}=\frac{x}{4-x}$,②
①÷②得$y=\frac{S'}{S}=-\frac{1}{16}x^{2}+\frac{1}{4}x$.
∵AB=4,
∴x的取值范围是0<x<4.
(3)由
(2)知x的取值范围是0<x<4,
∴$y=\frac{S'}{S}=-\frac{1}{16}x^{2}+\frac{1}{4}x=-\frac{1}{16}(x-2)^{2}+\frac{1}{4}\leq\frac{1}{4}$,
∴$S'\leq\frac{1}{4}S$,
∴$S\geq4S'$,
∴S-4S'≥0,
∴S-4S'的最小值为0.
(1)
∵D为AB的中点,
∴AB=2AD.
∵DE//BC,
∴AE=EC.
∵△ADE的边AE上的高和△CED的边CE上的高相等,
∴$S_{\triangle ADE}=S_{\triangle CDE}=S'$.
∵DE//BC,
∴△ADE∽△ABC,
∴$\frac{S_{\triangle ADE}}{S_{\triangle ABC}}=(\frac{AD}{AB})^{2}=\frac{1}{4}$,
∴$\frac{S'}{S}=\frac{1}{4}$.
(2)
∵AB=4,AD=x,
∴$\frac{S_{\triangle ADE}}{S_{\triangle ABC}}=\frac{x^{2}}{16}$①
∵DE//BC,
∴△ADE∽△ABC,
∴$\frac{AD}{AB}=\frac{AE}{AC}$.
∵AB=4,AD=x,
∴$\frac{AE}{AC}=\frac{x}{4}$,
∴$\frac{AE}{CE}=\frac{x}{4-x}$.
∵△ADE的边AE上的高和△CED的边CE上的高相等,
∴$\frac{S_{\triangle ADE}}{S_{\triangle CDE}}=\frac{AE}{CE}=\frac{x}{4-x}$,②
①÷②得$y=\frac{S'}{S}=-\frac{1}{16}x^{2}+\frac{1}{4}x$.
∵AB=4,
∴x的取值范围是0<x<4.
(3)由
(2)知x的取值范围是0<x<4,
∴$y=\frac{S'}{S}=-\frac{1}{16}x^{2}+\frac{1}{4}x=-\frac{1}{16}(x-2)^{2}+\frac{1}{4}\leq\frac{1}{4}$,
∴$S'\leq\frac{1}{4}S$,
∴$S\geq4S'$,
∴S-4S'≥0,
∴S-4S'的最小值为0.
查看更多完整答案,请扫码查看


