1. 若⊙O的半径为5 cm,点A到圆心O的距离为6 cm,则(
A.点A在圆外
B.点A在圆上
C.点A在圆内
D.点A与⊙O的位置关系不确定
A
)A.点A在圆外
B.点A在圆上
C.点A在圆内
D.点A与⊙O的位置关系不确定
答案:
A
2. 如图,AD//BE//CF,AB= 3,BC= 6,DE= 2.5,则EF的长为(
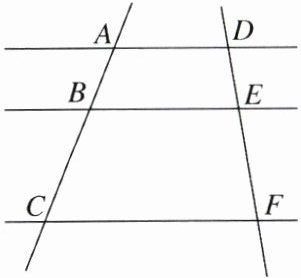
A.5
B.7.5
C.2.5
D.10
A
)
A.5
B.7.5
C.2.5
D.10
答案:
A
3. 二次函数$y= 2x^2$的图象一定过点(
A.(1,-2)
B.(-1,-2)
C.(-1,2)
D.(1,0)
C
)A.(1,-2)
B.(-1,-2)
C.(-1,2)
D.(1,0)
答案:
C
4. 小明的笔记本密码是一个两位数,他只记得第一位数是8,第二位数是一个奇数,则小明尝试一次就能正确打开笔记本的概率是(
A.$\frac{1}{10}$
B.$\frac{1}{5}$
C.$\frac{1}{4}$
D.$\frac{1}{2}$
B
)A.$\frac{1}{10}$
B.$\frac{1}{5}$
C.$\frac{1}{4}$
D.$\frac{1}{2}$
答案:
B
5. 下列命题中是真命题的为(
A.弦是直径
B.直径相等的两个圆是等圆
C.平面内的任意一点不在圆上就在圆内
D.一个圆有且只有一条直径
B
)A.弦是直径
B.直径相等的两个圆是等圆
C.平面内的任意一点不在圆上就在圆内
D.一个圆有且只有一条直径
答案:
B
6. 点D是线段AB的黄金分割点(AD>BD),若AB= 2,则AD= (
A.$\frac{\sqrt{5}-1}{2}$
B.$\frac{3-\sqrt{5}}{2}$
C.$\sqrt{5}-1$
D.$3-\sqrt{5}$
C
)A.$\frac{\sqrt{5}-1}{2}$
B.$\frac{3-\sqrt{5}}{2}$
C.$\sqrt{5}-1$
D.$3-\sqrt{5}$
答案:
C
7. 在同一平面直角坐标系中,函数$y= mx+m和y= -mx^2+2x+2$的图象可能是(
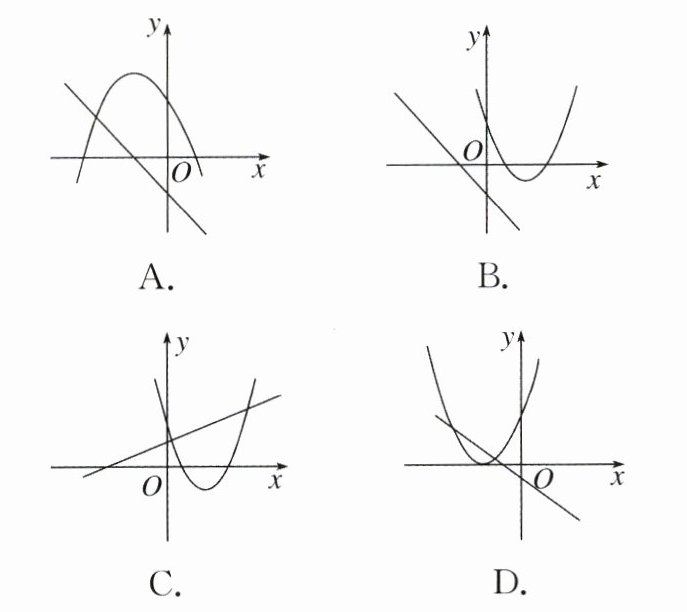
D
)
答案:
D
8. 如图,AB为⊙O的直径,点C在⊙O上,若AB= 4,AC= 2$\sqrt{2}$,则O到AC的距离为(

A.1
B.2
C.$\sqrt{2}$
D.2$\sqrt{2}$
C
)
A.1
B.2
C.$\sqrt{2}$
D.2$\sqrt{2}$
答案:
C
9. 抛物线$y= ax^2+bx+2$经过点A(m-1,n),B(-m-1,n),C(1,p),且p<2,则该抛物线的顶点在(
A.第一象限
B.第二象限
C.第三象限
D.第四象限
B
)A.第一象限
B.第二象限
C.第三象限
D.第四象限
答案:
B [解析]
∵抛物线$y=ax^{2}+bx+2$经过点$A(m - 1,n)$,$B( - m - 1,n)$,
∴该抛物线的对称轴为直线$x = \frac{(m - 1)+( - m - 1)}{2}=\frac{m - 1 - m - 1}{2} = - 1$,在y轴左侧,
∴$-\frac{b}{2a} = - 1$,
∴$b = 2a$。
∵抛物线$y=ax^{2}+bx+2$经过点$C(1,p)$,且$p<2$,
∴$a + b + 2<2$,
∴$a + b<0$,
∴$a + 2a<0$,
∴$a<0$,
∴该抛物线开口向下。
又
∵当$x = 0$时,$y = 2$,
∴该抛物线的顶点在第二象限。
∵抛物线$y=ax^{2}+bx+2$经过点$A(m - 1,n)$,$B( - m - 1,n)$,
∴该抛物线的对称轴为直线$x = \frac{(m - 1)+( - m - 1)}{2}=\frac{m - 1 - m - 1}{2} = - 1$,在y轴左侧,
∴$-\frac{b}{2a} = - 1$,
∴$b = 2a$。
∵抛物线$y=ax^{2}+bx+2$经过点$C(1,p)$,且$p<2$,
∴$a + b + 2<2$,
∴$a + b<0$,
∴$a + 2a<0$,
∴$a<0$,
∴该抛物线开口向下。
又
∵当$x = 0$时,$y = 2$,
∴该抛物线的顶点在第二象限。
查看更多完整答案,请扫码查看


