10. 如图,在$4×4$的正方形网格中,阴影部分构成一个轴对称图形,现在任意选取一个白色的小正方形涂上阴影,使阴影部分仍然构成一个轴对称图形的概率是(

A.$\frac{6}{13}$
B.$\frac{5}{13}$
C.$\frac{4}{13}$
D.$\frac{3}{13}$
B
) 
A.$\frac{6}{13}$
B.$\frac{5}{13}$
C.$\frac{4}{13}$
D.$\frac{3}{13}$
答案:
B
11. 小明外出游玩,带上棕色、蓝色、淡黄色3件上衣,他任意拿出1件上衣是棕色的概率是
$\frac{1}{3}$
.
答案:
$\frac{1}{3}$
12. 在篮球队员的选拔过程中,“投篮命中率”是一项重要的考核项目.如图,这是某篮球爱好者在平时运动过程中的投篮记录,请结合图示,估计现阶段该同学随机投篮一次正好命中的概率约为
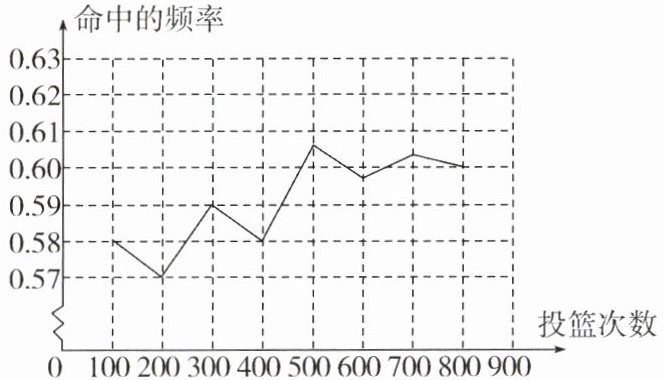
0.60
.(结果精确到0.01)
答案:
0.60
13. 先后两次抛掷同一枚质地均匀的硬币,则第一次正面向上、第二次反面向上的概率是
$\frac{1}{4}$
.
答案:
$\frac{1}{4}$
14. “平行四边形的对角线互相垂直平分”是
随机
事件.(填“必然”“不可能”或“随机”)
答案:
随机
15. 从标有1到20号的卡片中任意抽取一张,记事件“抽到2的倍数”发生的可能性为$P(A)$,事件“抽到5的倍数”发生的可能性为$P(B)$,事件“抽到13的倍数”发生的可能性为$P(C)$,则$P(A),P(B),P(C)$的大小关系为
$P(A) > P(B) > P(C)$
.(用“>”连接)
答案:
$P(A) > P(B) > P(C)$
16. 同时抛掷A,B两个均匀的小立方体(每个面上分别标有数字1,2,3,4,5,6),设两个小立方体朝上的数字分别为$x,y$,并以此确定点$P(x,y)$,那么点$P落在抛物线y= -x^2+3x$上的概率为
$\frac{1}{18}$
.
答案:
$\frac{1}{18}$
17. (8分)如图,下列第一排表示了10张扑克牌中的不同情况,任意摸1张,第二排的语言描述了摸到红色扑克牌的可能性大小,请用线连起来.


答案:
解:如图所示:
解:如图所示:

18. (8分)第一个盒中有2张白色卡片、1张黑色卡片,第二个盒中有1张白色卡片,2张黑色卡片,这些卡片除颜色外无其他差别,分别从每个盒中随机取出1张卡片.
(1)求在第一个盒中取出1张卡片是白色卡片的概率.
(2)用列表或画树状图的方法求取出的2张卡片都是黑色卡片的概率.
(1)求在第一个盒中取出1张卡片是白色卡片的概率.
(2)用列表或画树状图的方法求取出的2张卡片都是黑色卡片的概率.
答案:
解:
(1)在第一个盒中取出1张卡片是白色卡片的概率为$\frac{2}{3}$.
(2)列表如下:

由表知,共有9种等可能的结果,其中取出的2张卡片都是黑色卡片的有2种结果,
所以取出的2张卡片都是黑色卡片的概率为$\frac{2}{9}$.
解:
(1)在第一个盒中取出1张卡片是白色卡片的概率为$\frac{2}{3}$.
(2)列表如下:

由表知,共有9种等可能的结果,其中取出的2张卡片都是黑色卡片的有2种结果,
所以取出的2张卡片都是黑色卡片的概率为$\frac{2}{9}$.
查看更多完整答案,请扫码查看


