9. 如图,矩形ABCD被分割成3个全等的矩形. 若这3个矩形都和矩形ABCD相似,则$AD:AB= $(

A.3
B.$\sqrt{3}$
C.$\frac{3}{2}$
D.$\sqrt{5}$
B
)
A.3
B.$\sqrt{3}$
C.$\frac{3}{2}$
D.$\sqrt{5}$
答案:
B
10. 如图,在$Rt\triangle ABC$中,$\angle ACB= 90°$,$AB= 3$,D为直线AC左侧一点. 若$\triangle ABC \backsim \triangle CAD$,则$BC+CD$的最大值为(

A.$\frac{4}{3}$
B.$\frac{\sqrt{10}}{3}$
C.$\frac{\sqrt{5}}{2}$
D.$\frac{15}{4}$
D
)
A.$\frac{4}{3}$
B.$\frac{\sqrt{10}}{3}$
C.$\frac{\sqrt{5}}{2}$
D.$\frac{15}{4}$
答案:
D【解析】
∵△ABC∽△CAD,
∴$\frac{AB}{AC}=\frac{AC}{CD}$,
∴$\frac{3}{AC}=\frac{AC}{CD}$,
∴$CD=\frac{1}{3}AC^{2}$.
∵∠ACB=90°,
∴$AC^{2}=AB^{2}-BC^{2}=9-BC^{2}$,
∴$CD=\frac{1}{3}(9-BC^{2})=3-\frac{1}{3}BC^{2}$.
设BC=x,
∴$BC+CD=x+3-\frac{1}{3}x^{2}$
$=-\frac{1}{3}(x-\frac{3}{2})^{2}+\frac{15}{4}$,
∴当$x=\frac{3}{2}$时,BC+CD的最大值为$\frac{15}{4}$.
∵△ABC∽△CAD,
∴$\frac{AB}{AC}=\frac{AC}{CD}$,
∴$\frac{3}{AC}=\frac{AC}{CD}$,
∴$CD=\frac{1}{3}AC^{2}$.
∵∠ACB=90°,
∴$AC^{2}=AB^{2}-BC^{2}=9-BC^{2}$,
∴$CD=\frac{1}{3}(9-BC^{2})=3-\frac{1}{3}BC^{2}$.
设BC=x,
∴$BC+CD=x+3-\frac{1}{3}x^{2}$
$=-\frac{1}{3}(x-\frac{3}{2})^{2}+\frac{15}{4}$,
∴当$x=\frac{3}{2}$时,BC+CD的最大值为$\frac{15}{4}$.
11. 已知a,b,c,d是成比例线段,其中$a= 3\ cm$,$b= 2\ cm$,$d= 6\ cm$,则$c= $
9cm
.
答案:
9cm
12. 已知两个相似三角形对应角平分线的比为$4:3$,那么这两个三角形对应高的比是
4∶3
.
答案:
4∶3
13. 某品牌汽车为了打造更加精美的外观,特意将汽车倒车镜设计在整个车身黄金分割点的位置(如图),若车头与倒车镜的水平距离为2米,则该车车身总长约为

$(\sqrt{5}+3)$
米.(倒车镜到车尾部分较长,结果保留根号)
答案:
$(\sqrt{5}+3)$
14. 在下图所示的正方形网格中建立平面直角坐标系,已知每个小正方形的边长都是1,$\triangle ABC与\triangle A'B'C'$为位似图形,则位似中心的坐标为

(-4,-3)
.
答案:
(-4,-3)
15. 如图,在$\triangle ABC$中,G是三角形的重心,$AG= 5\ cm$,$GC= 12\ cm$,$AC= 13\ cm$,则$BG= $
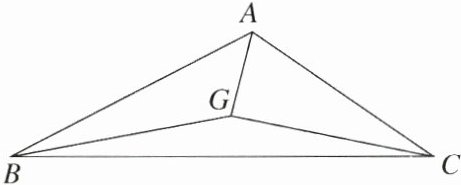
13
cm.
答案:
13
16. 如图,AB是半圆的直径,半径$OC \perp AB$于点O,AD平分$\angle CAB$,交$\overset{\frown}{BC}$于点D,连结CD,OD,给出下列结论:①$CE= OE$. ②$\triangle ODE \backsim \triangle ADO$. ③$2CD^2= CE \cdot AB$. 其中正确结论的序号是
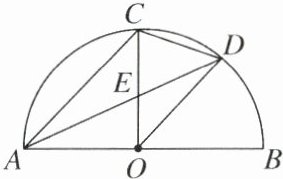
③
.
答案:
③【解析】对于①,过点E作EF⊥AC(图略),
∵OC⊥AB,AD平分∠CAB交$\overset{\frown}{BC}$于点D,
∴OE=EF.
在Rt△EFC中,CE>EF,
∴CE>OE,
∴①错误.
对于②,
∵在△ODE和△ADO中,只有∠ADO=∠EDO,
且∠COD=2∠CAD=2∠OAD,
∴∠DOE≠∠DAO,
不能得出△ODE∽△ADO,
∴②错误.
对于③,易知∠CAB=45°.
∵AD平分∠CAB交$\overset{\frown}{BC}$于点D,
∴∠CAD=$\frac{1}{2}×45^{\circ}=22.5^{\circ}$,
∴∠COD=45°.
∵AB是半圆的直径,
∴OC=OD,
∴∠OCD=∠ODC=67.5°.
∵OA=OD,
∴∠ADO=∠OAD=$\frac{1}{2}$∠COD=22.5°,
∴∠CDE=∠ODC-∠ADO=67.5°-22.5°=45°,
∴△CED∽△CDO,
∴$\frac{CD}{CO}=\frac{CE}{CD}$,
∴$CD^{2}=OC\cdot CE=\frac{1}{2}AB\cdot CE$,
∴$2CD^{2}=CE\cdot AB$.
∴③正确.
综上所述,只有③正确.
∵OC⊥AB,AD平分∠CAB交$\overset{\frown}{BC}$于点D,
∴OE=EF.
在Rt△EFC中,CE>EF,
∴CE>OE,
∴①错误.
对于②,
∵在△ODE和△ADO中,只有∠ADO=∠EDO,
且∠COD=2∠CAD=2∠OAD,
∴∠DOE≠∠DAO,
不能得出△ODE∽△ADO,
∴②错误.
对于③,易知∠CAB=45°.
∵AD平分∠CAB交$\overset{\frown}{BC}$于点D,
∴∠CAD=$\frac{1}{2}×45^{\circ}=22.5^{\circ}$,
∴∠COD=45°.
∵AB是半圆的直径,
∴OC=OD,
∴∠OCD=∠ODC=67.5°.
∵OA=OD,
∴∠ADO=∠OAD=$\frac{1}{2}$∠COD=22.5°,
∴∠CDE=∠ODC-∠ADO=67.5°-22.5°=45°,
∴△CED∽△CDO,
∴$\frac{CD}{CO}=\frac{CE}{CD}$,
∴$CD^{2}=OC\cdot CE=\frac{1}{2}AB\cdot CE$,
∴$2CD^{2}=CE\cdot AB$.
∴③正确.
综上所述,只有③正确.
查看更多完整答案,请扫码查看


