17.(8分)已知$\frac{a}{b}= \frac{2}{5}$.
(1)求代数式$\frac{a+4b}{2a-3b}$的值.
(2)当$2a+3b-3= 35$时,求a,b的值.
(1)求代数式$\frac{a+4b}{2a-3b}$的值.
(2)当$2a+3b-3= 35$时,求a,b的值.
答案:
解:
∵$\frac{a}{b}=\frac{2}{5}$,
∴令a=2k,b=5k,
(1)$\frac{a+4b}{2a-3b}$
=$\frac{2k+4×5k}{2×2k-3×5k}$
=$\frac{22k}{-11k}$
=-2.
(2)当2a+3b-3=35时,
2×2k+3×5k-3=35,
∴k=2,
∴a=2k=4,b=5k=10.
∵$\frac{a}{b}=\frac{2}{5}$,
∴令a=2k,b=5k,
(1)$\frac{a+4b}{2a-3b}$
=$\frac{2k+4×5k}{2×2k-3×5k}$
=$\frac{22k}{-11k}$
=-2.
(2)当2a+3b-3=35时,
2×2k+3×5k-3=35,
∴k=2,
∴a=2k=4,b=5k=10.
18.(8分)在一矩形ABCD的花坛四周修筑小路,使得相对两条小路的宽均相等. 花坛$AB= 20$米,$AD= 30$米,试问小路的宽x与y的比值为多少时,能使小路四周所围成的矩形$A'B'C'D' \backsim$矩形ABCD?请说明理由.


答案:
解:由题意有$\frac{20}{20+2y}=\frac{30}{30+2x}$,
从而有20(30+2x)=30(20+2y),解得$\frac{x}{y}=\frac{3}{2}$.
从而有20(30+2x)=30(20+2y),解得$\frac{x}{y}=\frac{3}{2}$.
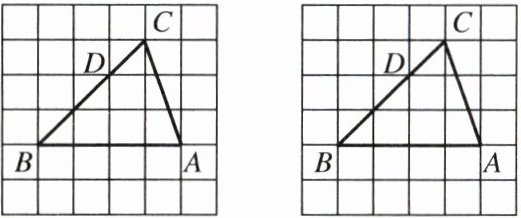
19.(8分)如图,由边长为1的小正方形组成的$6 × 6$网格中,$\triangle ABC$的顶点都在格点上,点D在BC边上,且$BD= 2CD$.
(1)BD的长等于______.
(2)请你仅用无刻度的直尺在边AB上找点E,使得$\triangle BDE与\triangle ABC$相似.(要求画出两种情形)
(1)BD的长等于______.
(2)请你仅用无刻度的直尺在边AB上找点E,使得$\triangle BDE与\triangle ABC$相似.(要求画出两种情形)

答案:
解:
(1)$2\sqrt{2}$
(2)如图1,2,△BDE即为所求.


解:
(1)$2\sqrt{2}$
(2)如图1,2,△BDE即为所求.


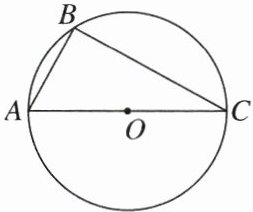
20.(8分)如图,AC是$\odot O$的直径,点B在$\odot O$上,$\angle ACB= 30^\circ$.
(1)利用尺规作$\angle ABC$的平分线BD,交AC于点E,交$\odot O$于点D,连结CD.(保留作图痕迹,不写作法)
(2)在(1)所作的图形中,求$\triangle ABE与\triangle CDE$的面积之比.
(1)利用尺规作$\angle ABC$的平分线BD,交AC于点E,交$\odot O$于点D,连结CD.(保留作图痕迹,不写作法)
(2)在(1)所作的图形中,求$\triangle ABE与\triangle CDE$的面积之比.

答案:
解:
(1)如图所示.
(2)如图,连结OD,设⊙O的半径为r.
在△ABE和,△DCE中
$\begin{cases}∠BAE=∠CDE, \\∠AEB=∠DEC,\end{cases}$
∴△ABE∽△DCE.
∵在Rt△ABC中,∠ABC=90°,∠ACB=30°,
∴AB=$\frac{1}{2}$AC=r.
∵BD平分∠ABC,
∴∠ABD=∠CBD=45°.
又
∵∠ABD=∠ACD,OD=OC,∠ACD=∠ODC=45°,
∴∠DOC=90°.
∵在Rt△ODC中,DC=$\sqrt{OD^{2}+OC^{2}}=\sqrt{2}r$,
∴$\frac{S_{\triangle ABE}}{S_{\triangle CDE}}=(\frac{AB}{DC})^{2}=(\frac{r}{\sqrt{2}r})^{2}=\frac{1}{2}$.

解:
(1)如图所示.
(2)如图,连结OD,设⊙O的半径为r.
在△ABE和,△DCE中
$\begin{cases}∠BAE=∠CDE, \\∠AEB=∠DEC,\end{cases}$
∴△ABE∽△DCE.
∵在Rt△ABC中,∠ABC=90°,∠ACB=30°,
∴AB=$\frac{1}{2}$AC=r.
∵BD平分∠ABC,
∴∠ABD=∠CBD=45°.
又
∵∠ABD=∠ACD,OD=OC,∠ACD=∠ODC=45°,
∴∠DOC=90°.
∵在Rt△ODC中,DC=$\sqrt{OD^{2}+OC^{2}}=\sqrt{2}r$,
∴$\frac{S_{\triangle ABE}}{S_{\triangle CDE}}=(\frac{AB}{DC})^{2}=(\frac{r}{\sqrt{2}r})^{2}=\frac{1}{2}$.

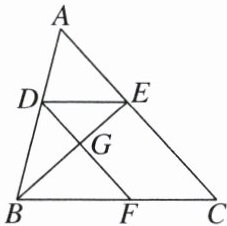
21.(8分)如图,在$\triangle ABC$中,点D,E,F分别在边AB,AC,BC上,连结DE,DF,BE,DF与BE相交于点G. 已知四边形DFCE是平行四边形,且$\frac{DE}{BC}= \frac{2}{5}$.
(1)若$AC= 25$,求线段AE,GF的长.
(2)若四边形GFCE的面积为48,求$\triangle EBC$的面积.
(1)若$AC= 25$,求线段AE,GF的长.
(2)若四边形GFCE的面积为48,求$\triangle EBC$的面积.

答案:
解:
(1)
∵四边形DFCE是平行四边形,
∴DE//BC,DF//AC,DE=CF,
∴△ADE∽△ABC,
∴$\frac{AE}{AC}=\frac{DE}{BC}=\frac{2}{5}$.
∵AC=25,
∴AE=10,
∴CE=25-10=15.
∵$\frac{DE}{BC}=\frac{CF}{BC}=\frac{2}{5}$,
∴$\frac{BF}{BC}=\frac{3}{5}$.
∵DF//AC,
∴△BFG∽△BCE,
∴$\frac{FG}{CE}=\frac{BF}{BC}=\frac{3}{5}$,
∴GF=9.
(2)
∵△BFG∽△BCE,$\frac{BF}{BC}=\frac{3}{5}$,
∴$\frac{S_{\triangle BFG}}{S_{\triangle BCE}}=(\frac{3}{5})^{2}=\frac{9}{25}$.
∵$S_{\triangle BFG}+S_{四边形GFCE}=S_{\triangle BCE}$,
∴$\frac{S_{四边形GFCE}}{S_{\triangle BCE}}=\frac{25-9}{25}=\frac{16}{25}$.
∵$S_{四边形GFCE}=48$,
∴$S_{\triangle BCE}=75$.
(1)
∵四边形DFCE是平行四边形,
∴DE//BC,DF//AC,DE=CF,
∴△ADE∽△ABC,
∴$\frac{AE}{AC}=\frac{DE}{BC}=\frac{2}{5}$.
∵AC=25,
∴AE=10,
∴CE=25-10=15.
∵$\frac{DE}{BC}=\frac{CF}{BC}=\frac{2}{5}$,
∴$\frac{BF}{BC}=\frac{3}{5}$.
∵DF//AC,
∴△BFG∽△BCE,
∴$\frac{FG}{CE}=\frac{BF}{BC}=\frac{3}{5}$,
∴GF=9.
(2)
∵△BFG∽△BCE,$\frac{BF}{BC}=\frac{3}{5}$,
∴$\frac{S_{\triangle BFG}}{S_{\triangle BCE}}=(\frac{3}{5})^{2}=\frac{9}{25}$.
∵$S_{\triangle BFG}+S_{四边形GFCE}=S_{\triangle BCE}$,
∴$\frac{S_{四边形GFCE}}{S_{\triangle BCE}}=\frac{25-9}{25}=\frac{16}{25}$.
∵$S_{四边形GFCE}=48$,
∴$S_{\triangle BCE}=75$.
查看更多完整答案,请扫码查看


