1. 画圆时圆规两脚间可叉开的距离是圆的(
A.直径
B.半径
C.周长
D.面积
B
)A.直径
B.半径
C.周长
D.面积
答案:
B
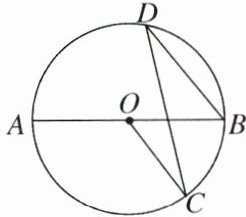
2. 如图,AB是⊙O的直径,∠D= 32°,则∠BOC等于(
A.126°
B.116°
C.58°
D.64°
D
)
A.126°
B.116°
C.58°
D.64°
答案:
D
3. 如图,AB是⊙O的直径,弦CD⊥AB于点E,OC= 5 cm,CD= 8 cm,则OE= (

A.8 cm
B.5 cm
C.3 cm
D.2 cm
C
)
A.8 cm
B.5 cm
C.3 cm
D.2 cm
答案:
C
4. 下列说法中,不正确的是(
A.圆的对称轴有无数条
B.把一个圆绕圆心旋转任意一个角度,仍会与原来的圆重合
C.平分弦的直径垂直于弦,并且平分弦所对的两条弧
D.在同圆或等圆中,长度相等的两条弧是等弧
C
)A.圆的对称轴有无数条
B.把一个圆绕圆心旋转任意一个角度,仍会与原来的圆重合
C.平分弦的直径垂直于弦,并且平分弦所对的两条弧
D.在同圆或等圆中,长度相等的两条弧是等弧
答案:
C
5. 如图,将△ABC绕点A逆时针旋转一定的度数,得到△ADE.若点D在线段BC的延长线上,∠B= 35°,则旋转的度数为(

A.100°
B.110°
C.145°
D.55°
B
)
A.100°
B.110°
C.145°
D.55°
答案:
B
6. 如图,△ABC是⊙O的内接三角形,若∠A= 60°,BC= 2√3,则⊙O的半径长为( )

A.4
B.√3
C.2
D.1

A.4
B.√3
C.2
D.1
答案:
C 【解析】如图,连结 OF.
∵DE⊥AB,AB 为⊙O 的直径,
∴DE=EF,$\overset{\frown}{AD}=\overset{\frown}{AF}$.
∵D 是弧 AC 的中点,
∴$\overset{\frown}{AD}=\overset{\frown}{CD}$,
∴$\overset{\frown}{AC}=\overset{\frown}{DF}$,
∴AC=DF=12,
∴EF=$\frac{1}{2}$DF=6.设 OA=OF=r,
在 Rt△OEF 中,则有$r^{2}=6^{2}+(r-3)^{2}$,
解得$r=\frac{15}{2}$,
∴OE=OA - AE=$\frac{15}{2}-3=\frac{9}{2}=4.5$.

C 【解析】如图,连结 OF.
∵DE⊥AB,AB 为⊙O 的直径,
∴DE=EF,$\overset{\frown}{AD}=\overset{\frown}{AF}$.
∵D 是弧 AC 的中点,
∴$\overset{\frown}{AD}=\overset{\frown}{CD}$,
∴$\overset{\frown}{AC}=\overset{\frown}{DF}$,
∴AC=DF=12,
∴EF=$\frac{1}{2}$DF=6.设 OA=OF=r,
在 Rt△OEF 中,则有$r^{2}=6^{2}+(r-3)^{2}$,
解得$r=\frac{15}{2}$,
∴OE=OA - AE=$\frac{15}{2}-3=\frac{9}{2}=4.5$.

7. 如图,AB为⊙O的直径,D是弧AC的中点,过点D作DE⊥AB于点E,延长DE交⊙O于点F,若AE= 3,AC= 12,则线段OE的长为(

A.5
B.4
C.4.5
D.3
D
)
A.5
B.4
C.4.5
D.3
答案:
D
查看更多完整答案,请扫码查看


