8. 已知二次函数 $y= x^2-2x-4$,当自变量 $x$ 的取值范围是 $x\geq-1$ 时,下列关于函数 $y$ 的最值的说法正确的是(
A.有最小值 $-5$,有最大值 $-1$
B.有最小值 $-5$,无最大值
C.有最小值 $-1$,无最大值
D.无最小值,有最大值 $-1$
B
)A.有最小值 $-5$,有最大值 $-1$
B.有最小值 $-5$,无最大值
C.有最小值 $-1$,无最大值
D.无最小值,有最大值 $-1$
答案:
B
9. 如图,已知 $AB$ 是 $\odot O$ 的直径,$AD$ 切 $\odot O$ 于点 $A$,$\widehat{EC}= \widehat{CB}$,则下列结论中不一定正确的是(
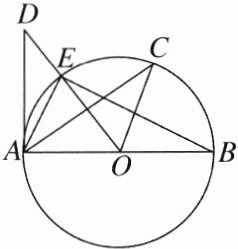
A.$BA\perp DA$
B.$OC// AE$
C.$\angle COE= 2\angle CAE$
D.$OD\perp AC$
D
) 
A.$BA\perp DA$
B.$OC// AE$
C.$\angle COE= 2\angle CAE$
D.$OD\perp AC$
答案:
D
10. 已知二次函数 $y= -x^2+3mx-3n$ 的图象与 $x$ 轴没有交点,则(
A.$2m+n>\frac{4}{3}$
B.$2m+n<\frac{4}{3}$
C.$2m-n<\frac{4}{3}$
D.$2m-n>\frac{4}{3}$
C
)A.$2m+n>\frac{4}{3}$
B.$2m+n<\frac{4}{3}$
C.$2m-n<\frac{4}{3}$
D.$2m-n>\frac{4}{3}$
答案:
C
11. 已知线段 $a,b,c,d$ 是成比例线段,其中 $a= 6$,$b= 3$,$c= 2$,则 $d$ 的值是
1
.
答案:
1
12. 若二次函数 $y= ax^2$ 的图象经过点 $(-2,8)$,则 $a$ 的值为
2
.
答案:
2
13. 某试验小组做了可转动转盘(如图),想求当转盘停止转动后,“指针落在灰色区域内”的概率,试验数据如下表:
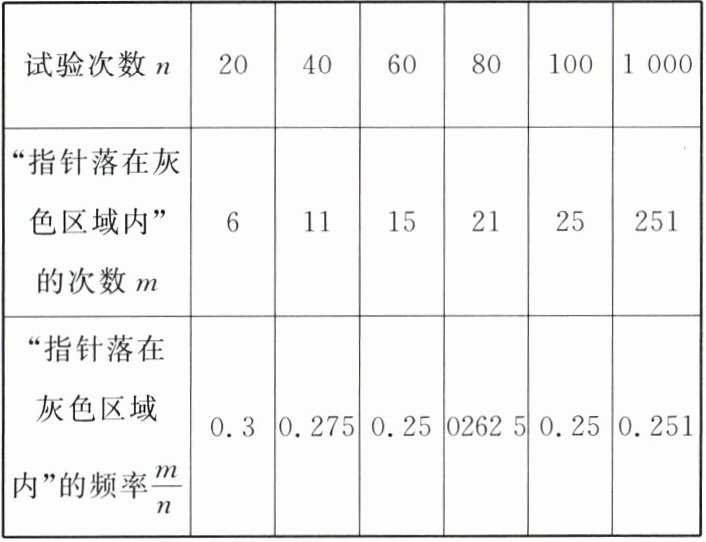
根据表格,可以估计出转动转盘一次,当转盘停止转动后,“指针落在灰色区域内”的概率约是
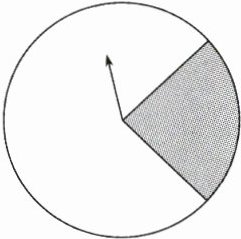

根据表格,可以估计出转动转盘一次,当转盘停止转动后,“指针落在灰色区域内”的概率约是
0.25
.(结果精确到 0.01)
答案:
0.25
14. 如图,折扇的骨柄 $OA$ 长 27 cm,打开后 $\angle AOB$ 为 $160°$,则图中弧 $AB$ 的长为

24π
cm.(结果保留 $\pi$)
答案:
24π
15. 已知抛物线 $y= -x^2-3x+3$,点 $P(m,n)$ 在抛物线上,则 $m+n$ 的最大值是
4
.
答案:
4
16. 如图,将正方形 $ABCD$ 的边 $AB$,$BC$ 绕着点 $A$ 逆时针旋转一定角度,得到线段 $AB'$,$B'C'$,连结 $AC'$ 交 $CD$ 于点 $E$,连结 $BB'$,$CC'$,若 $\triangle ABB'\sim\triangle CEC'$,则 $\angle ABB'= $______.


答案:
75° [解析]如图,连结AC.

根据旋转的性质得 $AB=AB'$,$AC=AC'$,
$\therefore \angle ABB'=\angle AB'B$,$\angle ACC'=\angle AC'C$,
$\because \triangle ABB'\backsim \triangle CEC'$,$\therefore \angle ABB'=\angle CEC'$。
设 $\angle ABB'=\angle AB'B=\angle CEC'=\angle AC'C= \angle ACC'=x$,
$\therefore \angle CAC'=180^{\circ}-2x$,$\angle AED=\angle CEC'=x$,
$\therefore \angle EAD=90^{\circ}-x$。
$\because$ 四边形ABCD是正方形,
$\therefore \angle CAD=45^{\circ}$,
$\therefore \angle CAC'+\angle EAD=45^{\circ}$,
即 $180^{\circ}-2x+90^{\circ}-x=45^{\circ}$,
$\therefore x=75^{\circ}$,$\therefore \angle ABB'=75^{\circ}$。
75° [解析]如图,连结AC.

根据旋转的性质得 $AB=AB'$,$AC=AC'$,
$\therefore \angle ABB'=\angle AB'B$,$\angle ACC'=\angle AC'C$,
$\because \triangle ABB'\backsim \triangle CEC'$,$\therefore \angle ABB'=\angle CEC'$。
设 $\angle ABB'=\angle AB'B=\angle CEC'=\angle AC'C= \angle ACC'=x$,
$\therefore \angle CAC'=180^{\circ}-2x$,$\angle AED=\angle CEC'=x$,
$\therefore \angle EAD=90^{\circ}-x$。
$\because$ 四边形ABCD是正方形,
$\therefore \angle CAD=45^{\circ}$,
$\therefore \angle CAC'+\angle EAD=45^{\circ}$,
即 $180^{\circ}-2x+90^{\circ}-x=45^{\circ}$,
$\therefore x=75^{\circ}$,$\therefore \angle ABB'=75^{\circ}$。
查看更多完整答案,请扫码查看


