《2025年精彩练习就练这一本九年级数学全一册浙教版评议教辅》

17. (8分)如图,已知AB为⊙O的直径,弦CD⊥AB,$\overset{\frown}{AC}= \overset{\frown}{CE}$,AE交CD于F.求证:CF= AF.

答案：
证明:如图，连结 AC.
∵AB 为⊙O 的直径，
弦 CD⊥AB,
∴$\overset{\frown}{AC}=\overset{\frown}{AD}$.
∵$\overset{\frown}{AC}=\overset{\frown}{CE}$,
∴$\overset{\frown}{AD}=\overset{\frown}{CE}$,
∴∠C=∠CAF,
∴CF=AF.

18. (8分)在下图所示的网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的坐标分别为A(0,1),B(-3,5),C(-3,1).
(1)在图中画出△ABC以点A为旋转中心,按顺时针方向旋转90°后的$△AB_1C_1.$
(2)在图中画出与△ABC关于原点对称的$△A_2B_2C_2,$并写出$B_2,C_2$两点的坐标.

答案：
解:
(1)如图，△AB₁C₁即为所求.

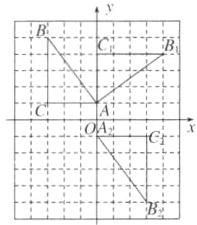
(2)如图，△A₂B₂C₂即为所求，B₂(3，-5),C₂(3，-1).

19. (8分)已知正六边形ABCDEF的中心为O,外接圆的半径OA= 6.
(1)求正六边形的边长.
(2)以A为圆心,AF为半径画弧BF,求$\overset{\frown}{BF}$的长.

答案： 解:
(1)
∵六边形 ABCDEF 是正六边形，
∴正六边形的边长=外接圆的半径 OA=6.
(2)
∵六边形 ABCDEF 是正六边形，
∴∠BAF=120°,
∴$\overset{\frown}{BF}$的长=$\frac{120\pi×6}{180}=4\pi$.

20. (8分)如图,AB是⊙O的弦,C是$\overset{\frown}{AB}$的中点.
(1)连结OC,求证:OC垂直平分AB.
(2)若AB= 8,AC= 2√5,求⊙O的半径.

答案：
解:
(1)证明:连结 OC,如图.
∵OC 是⊙O 的半径，C 是$\overset{\frown}{AB}$的中点，
∴$\overset{\frown}{AC}=\overset{\frown}{BC}$,
∴OC 垂直平分 AB.
(2)连结 OA,如图，
由
(1)知，OC 垂直平分 AB,
∵AB=8,AC=$2\sqrt{5}$,
∴AD=$\frac{1}{2}$AB=4,
∴CD=$\sqrt{AC^{2}-AD^{2}}=\sqrt{(2\sqrt{5})^{2}-4^{2}}=2$,
设⊙O 的半径为 r,
则 OD=r - 2,OA=r,在 Rt△AOD 中，
$AD^{2}+OD^{2}=OA^{2}$,即$4^{2}+(r - 2)^{2}=r^{2}$,
解得 r=5.