《2025年精彩练习就练这一本九年级数学全一册浙教版评议教辅》

9. 工人师傅将截面为矩形的木条锯成矩形ABCD和矩形AEFG两部分,如图所示,C,B,G在一条直线上,CB= a,BG= b,∠AGB= β,则点E到CG的距离等于( )


A.$a\cos\beta + b\sin\beta$
B.$a\sin\beta + b\tan\beta$
C.$a\cos\beta + b\tan\beta$
D.$b\sin\beta + a\tan\beta$

答案：
C [解析]如图,过点E作EH⊥BA,交BA的延长线于点H.

∵∠BAG+∠AGB=90°,∠BAG+∠HAE=90°,
∴∠HAE=∠AGB=β.
∵BG=b,tanβ=$\frac{AB}{b}$,
∴AB=btanβ.
∵AE=AD=BC=a,
∴cosβ=$\frac{AH}{a}$,
∴AH=acosβ.
∴HB=AH+AB=acosβ+btanβ.

10. 如图,在湖边高出水面50 m的山顶A处看见一架无人机停留在湖面上空某处,观测到无人机底部标志P处的仰角为45°,又观其在湖中之像P'的俯角为60°,则无人机到湖面的距离为(D)

A.$(25\sqrt{3}+75)$m
B.$(50\sqrt{3}+50)$m
C.$(75\sqrt{3}+75)$m
D.$(50\sqrt{3}+100)$m

答案： D [解析]设AE=xm.
在Rt△AEP中,∠PAE=45°,
则∠P=45°,
∴PE=AE=xm.
∵山顶A处高出湖面50m，
∴OE=50m,
∴OP'=OP=PE+OE=(x+50)m.
∵∠P'AE=60°,
∴P'E=tan60°·AE=$\sqrt{3}$xm,
∴OP'=P'E−OE=($\sqrt{3}$x−50)m,
∴x+50=($\sqrt{3}$x−50),
解得x=50($\sqrt{3}$+1),
∴PO=PE+OE=50($\sqrt{3}$+1)+50
=50$\sqrt{3}$+100(m),
即无人机到湖面的距离是(50$\sqrt{3}$+100)m.

11. 已知α是锐角,如果$\sin\alpha=\frac{1}{2}$,那么α= 30°.

答案： 30°

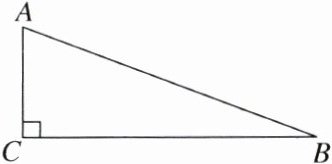
12. 如图,在Rt△ABC中,∠C= 90°,BC= 3AC,则tan B= $\frac{1}{3}$.

答案： $\frac{1}{3}$

13. 如图,在△ABC中,BC= $\sqrt{6}+\sqrt{2}$,∠C= 45°,AB= $\sqrt{2}$AC,则AC的长为2.

答案： 2

14. 如图,在这个正方形网格中,每个小正方形的边长均为1个单位长度,A,B,C,D都在格点上,AB与CD相交于点O,则tan∠BOD的值等于3.

答案： 3

15. 已知在△ABC中,$\tan B= \frac{2}{3}$,BC= 6,过点A作AD⊥BC于点D,且满足BD∶CD= 2∶1,则△ABC的面积为8或24.

答案： 8或24

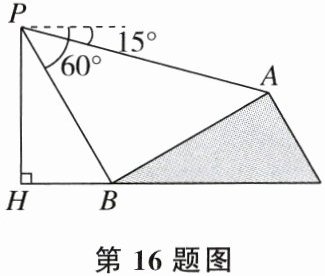
16. 如图,小明在距离地面30米的P处测得A处的俯角为15°,B处的俯角为60°.若斜面坡比为1∶$\sqrt{3}$,则斜坡AB的长是20$\sqrt{3}$米.

答案： 20$\sqrt{3}$

17.(8分)计算：
(1)$\cos^2 45^\circ - \sin^2 30^\circ$.
(2)$-1^{2024} + 3\tan 30^\circ$.

答案： 解:
(1)$\cos^2 45^\circ - \sin^2 30^\circ$=($\frac{\sqrt{2}}{2}$)²−($\frac{1}{2}$)²=$\frac{2}{4}$−$\frac{1}{4}$=$\frac{1}{4}$.
(2)$-1^{2024} + 3\tan 30^\circ$=−1+3×$\frac{\sqrt{3}}{3}$=−1+$\sqrt{3}$.