《2025年精彩练习就练这一本九年级数学全一册浙教版评议教辅》

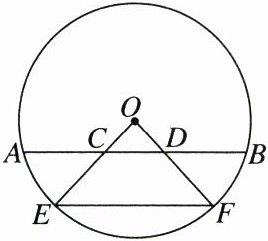
21. (8分)如图,⊙O的弦AB与半径OE,OF分别相交于C,D两点,AC= BD.求证:
(1)OC= OD.
(2)$\overset{\frown}{AE}= \overset{\frown}{BF}$.

答案：
证明:
(1)连结 OA,OB,如图.
∴∠OAC=∠OBD.
在△OAC 与△OBD 中，
$\left\{\begin{array}{l} OA=OB,\\ ∠OAC=∠OBD,\\ AC=BD,\end{array}\right.$
∴△OAC≌△OBD(SAS).
∴OC=OD.
(2)由
(1)可知，△OAC≌△OBD,
∴∠AOC=∠BOD,
∴$\overset{\frown}{AE}=\overset{\frown}{BF}$.

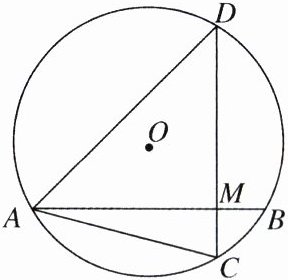
22. (10分)如图,线段AB,CD是⊙O的两条弦,AB= CD,连结AD,AC.
(1)证明:AM= DM.
(2)若AB⊥CD于点M,且弦AC的弦心距为4,求⊙O的半径.

答案：
解:
(1)证明:
∵AB=CD,
∴$\overset{\frown}{AB}=\overset{\frown}{CD}$,
∴$\overset{\frown}{AC}=\overset{\frown}{BD}$,
∴∠DAM=∠D,
∴AM=DM.
(2)连结 OA,OC,过点 O 作 ON⊥AC 于点 N,
∵AB⊥CD 于点 M,AM=DM,
∴∠D=45°,
∴∠AOC=90°,
∴ON=AN=4,
∴OA=$\sqrt{AN^{2}+ON^{2}}=\sqrt{4^{2}+4^{2}}=4\sqrt{2}$,
即⊙O 的半径为$4\sqrt{2}$.

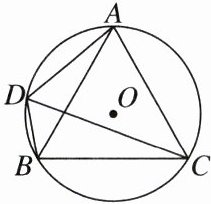
23. (10分)如图,⊙O为等边三角形ABC的外接圆,半径为2,点D在劣弧$\overset{\frown}{AB}$上运动(不与点A,B重合),连结DA,DB,DC.
(1)求证:DC是∠ADB的平分线.
(2)四边形ADBC的面积S是线段DC的长x的函数吗?如果是,求出函数表达式;如果不是,请说明理由.

答案：
解:
(1)证明:
∵△ABC 是等边三角形，
∴∠ABC=∠BAC=∠ACB=60°.
∵∠ADC=∠ABC=60°,∠BDC=∠BAC=60°,
∴∠ADC=∠BDC,
∴DC 是∠ADB 的平分线.
(2)四边形 ADBC 的面积 S 是线段 DC 的长 x 的函数，理由如下:
如图，将△ADC 绕点 C 逆时针旋转 60°,得到△BHC,
∴CD=CH,∠DAC=∠HBC.
∵四边形 ACBD 是圆内接四边形，
∴∠DAC+∠DBC=180°,
∴∠DBC+∠HBC=180°,
∴D,B,H 三点共线.
∵DC=CH,∠DCH=60°,
∴△DCH 是等边三角形.
∵四边形 ADBC 的面积$S=S_{\triangle ADC}+S_{\triangle BDC}=S_{\triangle CDH}=\frac{\sqrt{3}}{4}CD^{2}$,
∴$S=\frac{\sqrt{3}}{4}x^{2}(2\sqrt{3}＜x\leq4)$.

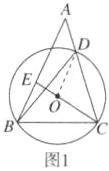
24. (12分)如图,在△ABC中,D在边AC上,圆O为锐角三角形BCD的外接圆,连结CO并延长交AB于点E.
(1)如图1,若∠DBC= α,请用含α的代数式表示∠DCE.
(2)如图2,过点B作BF⊥AC,垂足为F,BF与CE交于点G,已知∠ABD= ∠CBF.
①求证:EB= EG.
②若CE= 5,AC= 8,求FG+FB的值.

答案：
解:
(1)如图 1,连结 OD,
∵∠DOC=2∠DBC=2α,OD=OC,
∴∠DCE=90° - α.
(2)①证明:
∵∠ABD=∠CBF,
∴∠EBG=∠ABD+∠DBF=∠CBF+∠DBF=∠DBC,
设∠DBC=α,由
(1)得∠DCE =90° - α,
∵BF⊥AC,
∴∠FGC=∠BGE=α,
∴∠EBG=∠EGB,
∴EB=EG.
②如图 2,过点 E 分别作 EM⊥BF 于点 M,EN⊥AC 于点 N,由①得
∠EBG=α,∠ACE=90° - α,
∵BF⊥AC,
∴∠A=90° - α,
∴AE=CE=5.
∵EN⊥AC,AC=8,
∴CN=4,
∴EN=3.
∵EM⊥BF,NF⊥BF,EN⊥AC,
∴四边形 EMFN 为矩形，
∴EN=MF=3.
∵EB=EG,EM⊥BG,
∴BM=GM,
∴FG+FB=FM - MG+FM+BM=2FM=6.