1. 无理数
概 念:无限
特 征:(1)是无限小数;
(2)是不循环小数.
分 类:无理数分为正无理数和负无理数两类.
概 念:无限
不循环
小数称为无理数.特 征:(1)是无限小数;
(2)是不循环小数.
分 类:无理数分为正无理数和负无理数两类.
答案:
1.不循环
3. 实数
概 念:______和______统称实数,即实数可以分为______和______.
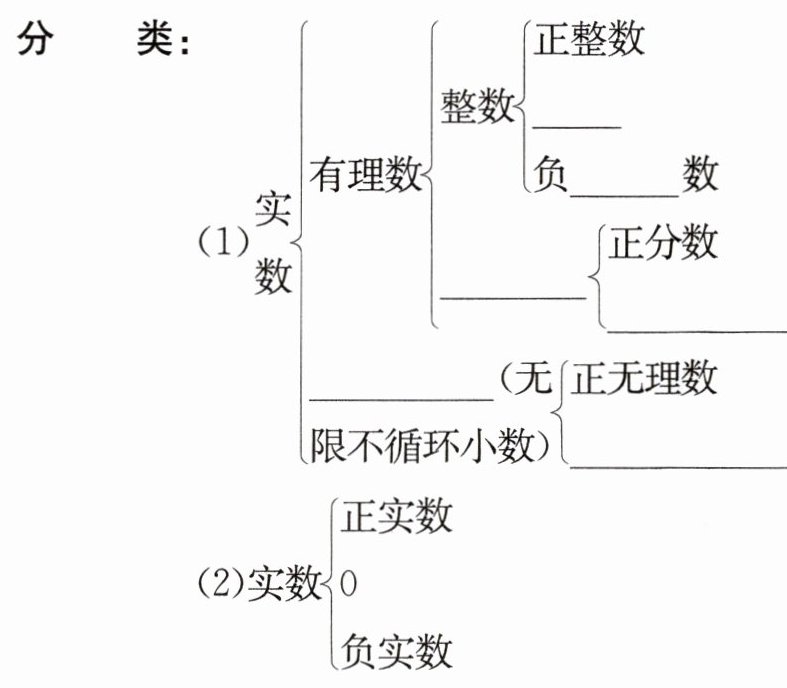
概 念:______和______统称实数,即实数可以分为______和______.

答案:
3.有理数 无理数 有理数 无理数 0 整 分数 负分数 无理数 负无理数
4. 实数范围内的相关概念
相反数:实数$a$的相反数为
倒 数:当$a\neq0$时,实数$a$的倒数为
绝对值:实数$a$的绝对值为
注 意:在实数范围内,相反数、倒数、绝对值的意义与有理数范围内的相反数、倒数、绝对值的意义完全一样. 实数和有理数一样,可以进行加、减、乘、除、乘方运算,而且有理数的运算法则与运算律对实数仍然适用.
相反数:实数$a$的相反数为
-a
.倒 数:当$a\neq0$时,实数$a$的倒数为
\frac{1}{a}
.绝对值:实数$a$的绝对值为
\vert a\vert
.注 意:在实数范围内,相反数、倒数、绝对值的意义与有理数范围内的相反数、倒数、绝对值的意义完全一样. 实数和有理数一样,可以进行加、减、乘、除、乘方运算,而且有理数的运算法则与运算律对实数仍然适用.
答案:
$4.-a \frac{1}{a} \vert a\vert$
5. 实数与数轴上的点的对应关系
关 系:事实上,每一个实数都可以用数轴上的
注 意:在数轴上,右边的点表示的数比左边的点表示的数大.
关 系:事实上,每一个实数都可以用数轴上的
一
个点表示;反过来,数轴上的每一个点都表示一个实数
.也就是说,实数和数轴上的点是一一对应
的.注 意:在数轴上,右边的点表示的数比左边的点表示的数大.
答案:
5.一 一个实数 一一对应
1. 下列实数中,无理数是(
A.$-3$
B.$0$
C.$\frac{2}{3}$
D.$\frac{\pi}{2}$
D
)A.$-3$
B.$0$
C.$\frac{2}{3}$
D.$\frac{\pi}{2}$
答案:
1.D
2. 如图,$A$,$B$,$C$,$D$是数轴上的四个点,其中最适合表示无理数$\pi$的点是(
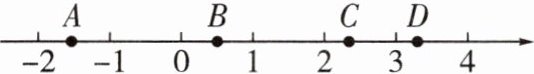
A.点$A$
B.点$B$
C.点$C$
D.点$D$
D
)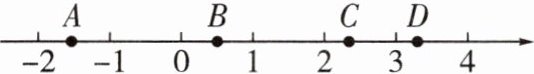
A.点$A$
B.点$B$
C.点$C$
D.点$D$
答案:
2.D
3. $-\frac{\pi}{4}$的相反数是
\frac{\pi}{4}
.
答案:
$3.\frac{\pi}{4}$
4. 化简:$\vert1 - \pi\vert=$
\pi-1
.
答案:
$4.\pi-1$
5. 下列各数中,哪些是有理数?哪些是无理数?
$0.275151151115\cdots$(相邻两个$5$之间$1$的个数逐次加$1$),$-\frac{3}{4}$,$\frac{23}{7}$,$3.141$,$0.24\dot{5}$,$\frac{\pi}{3}$.
$0.275151151115\cdots$(相邻两个$5$之间$1$的个数逐次加$1$),$-\frac{3}{4}$,$\frac{23}{7}$,$3.141$,$0.24\dot{5}$,$\frac{\pi}{3}$.
答案:
5.有理数:$-\frac{3}{4},\frac{23}{7},3.141,0.24\dot{5};$无理数:0.275 151 151 115···(相邻两个5之间1的个数逐次加$1),\frac{\pi}{3}$
查看更多完整答案,请扫码查看


