知识梳理
感受生活中存在着不能用有理数表示的数
拼 图:有两个边长为1的小正方形,剪一剪,拼一拼,能否拼成一个大的正方形?有如图所示的甲、乙、丙三种拼法。
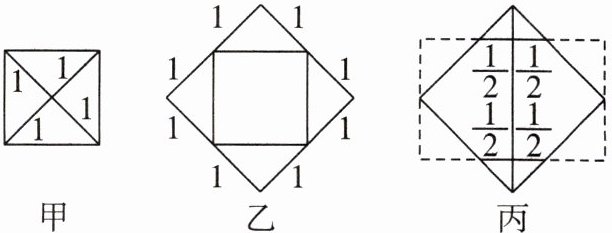
注 意:事实上,满足等式$a^{2}=2$的$a$既不是整数,也不是分数,所以$a$不是有理数。
勾股定理:如图,以直角三角形的斜边为边的正方形的面积为
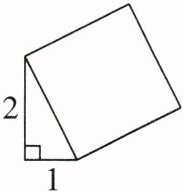
感受生活中存在着不能用有理数表示的数
拼 图:有两个边长为1的小正方形,剪一剪,拼一拼,能否拼成一个大的正方形?有如图所示的甲、乙、丙三种拼法。

注 意:事实上,满足等式$a^{2}=2$的$a$既不是整数,也不是分数,所以$a$不是有理数。
勾股定理:如图,以直角三角形的斜边为边的正方形的面积为
5
,设该正方形的边长为$b$,则$b^{2}=$5
,$b$不是有理数。
答案:
5 5
1. 下列正方形的边长不是有理数的是(
A.面积是1.96的正方形
B.面积是64的正方形
C.面积是$\frac{16}{25}$的正方形
D.面积是48的正方形
D
)A.面积是1.96的正方形
B.面积是64的正方形
C.面积是$\frac{16}{25}$的正方形
D.面积是48的正方形
答案:
1 D
2. 如图,在$\triangle ABC$中,$\angle C=90^{\circ}$,$AC=BC=1$,则$AB^{2}=$,$AB$的长
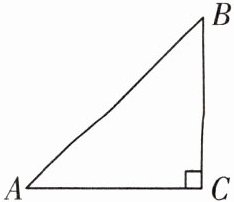
不是
整数,$AB$的长不是
分数。(填“是”或“不是”)
答案:
2 不是 不是
3. 一个直角三角形两条直角边的长分别是3和5,则斜边的长$a$是有理数吗?
答案:
3 a不是有理数
4. 若一个正方体的体积为4,则这个正方体的棱长是有理数吗?
答案:
4 这个正方体的棱长不是有理数
5. 如图,在$\triangle ABC$中,$CD\perp AB$,垂足为点$D$,$AC=6$,$AD=5$。$CD$的长可能是整数吗?可能是分数吗?可能是有理数吗?
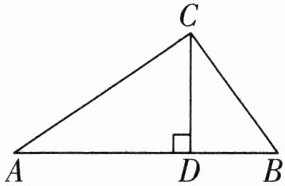

答案:
5 CD的长不可能是整数,不可能是分数,不可能是有理数
查看更多完整答案,请扫码查看


