知识梳理
1. 二元一次方程与一次函数的关系
关 系:一般地,以一个二元一次方程的解为坐标的点组成的图象与相应的
2. 二元一次方程组与一次函数的关系
关 系:一般地,从图形的角度看,确定两条直线交点的坐标,相当于求相应的二元一次方程组的解;解一个二元一次方程组相当于确定相应两条直线交点的坐标. 即二元一次方程组的解对应着平面上两条直线的交点.
1. 二元一次方程与一次函数的关系
关 系:一般地,以一个二元一次方程的解为坐标的点组成的图象与相应的
一次函数
的图象相同,是同一条直线. 即一个二元一次方程对应着平面上的一条直线.2. 二元一次方程组与一次函数的关系
关 系:一般地,从图形的角度看,确定两条直线交点的坐标,相当于求相应的二元一次方程组的解;解一个二元一次方程组相当于确定相应两条直线交点的坐标. 即二元一次方程组的解对应着平面上两条直线的交点.
答案:
1. 一次函数
1. 下面四条直线中,每个点的坐标都是二元一次方程 $2x - y = 2$ 的解的是 (
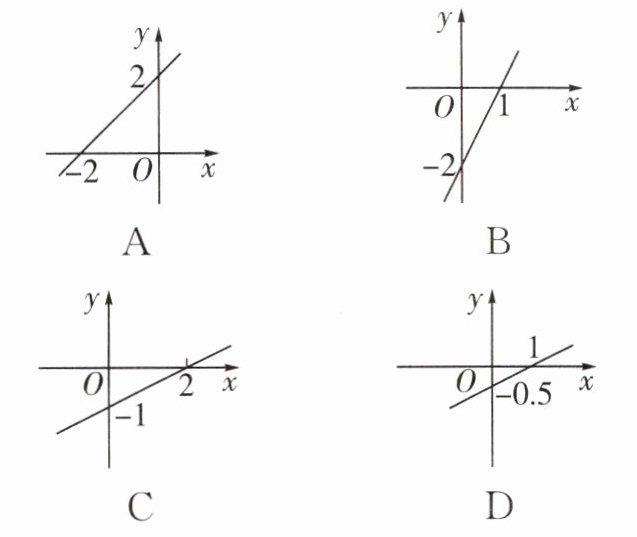
B
)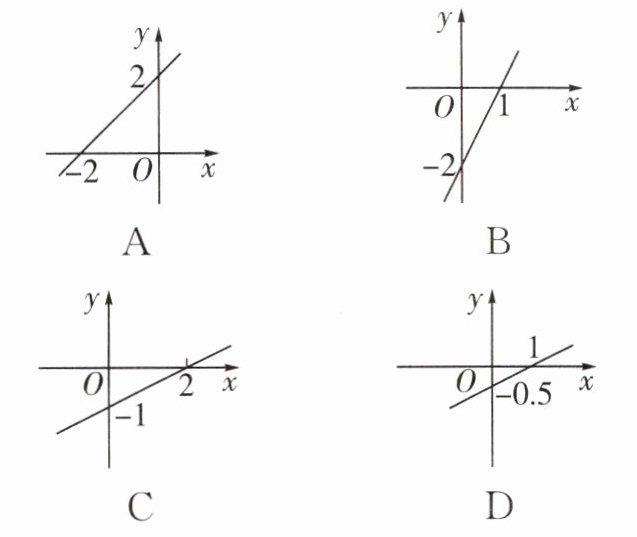
答案:
1.B
2. 已知一次函数 $y = 3x$ 与 $y = -\frac{3}{2}x + \frac{9}{2}$ 图象的交点坐标是 $(1, 3)$,则方程组 $\begin{cases}y = 3x,\\y = -\frac{3}{2}x + \frac{9}{2}\end{cases}$ 的解是 (
A.$\begin{cases}x = 2,\\y = 6\end{cases}$
B.$\begin{cases}x = -1,\\y = 3\end{cases}$
C.$\begin{cases}x = 0,\\y = 0\end{cases}$
D.$\begin{cases}x = 1,\\y = 3\end{cases}$
D
)A.$\begin{cases}x = 2,\\y = 6\end{cases}$
B.$\begin{cases}x = -1,\\y = 3\end{cases}$
C.$\begin{cases}x = 0,\\y = 0\end{cases}$
D.$\begin{cases}x = 1,\\y = 3\end{cases}$
答案:
2.D
3. 若关于 $x$,$y$ 的二元一次方程组 $\begin{cases}y = ax - 4,\\y = 4x + b\end{cases}$ 的解是 $\begin{cases}x = 2,\\y = 3,\end{cases}$ 则直线 $y = ax - 4$ 与 $y = 4x + b$ 的交点坐标是
(2, 3)
.
答案:
3.(2, 3)
4. 如图,已知直线 $l_1: y = 3x + 1$ 和直线 $l_2: y = mx + n$ 交于点 $P(1, b)$,则关于 $x$,$y$ 的二元一次方程组 $\begin{cases}y = mx + n,\\y = 3x + 1\end{cases}$ 的解是
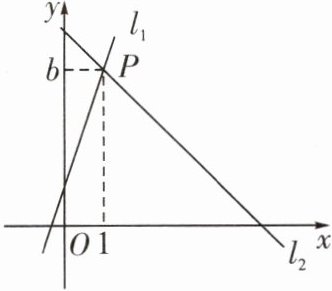
{
x = 1,
y = 4
}
.x = 1,
y = 4
}

答案:
4. {
x = 1,
y = 4
}
x = 1,
y = 4
}
5. 已知两直线 $y_1 = 2x - 3$,$y_2 = 6 - x$.
(1) 在同一坐标系中作出它们的图象;
(2) 求它们的交点 $A$ 的坐标;
(3) 根据图象指出当 $x$ 为何值时,$y_1 > y_2$,当 $x$ 为何值时,$y_1 < y_2$;
(4) 求这两条直线与 $x$ 轴所围成的三角形的面积.
(1) 在同一坐标系中作出它们的图象;
(2) 求它们的交点 $A$ 的坐标;
(3) 根据图象指出当 $x$ 为何值时,$y_1 > y_2$,当 $x$ 为何值时,$y_1 < y_2$;
(4) 求这两条直线与 $x$ 轴所围成的三角形的面积.
答案:
5.
(1)如图:

(2)交点A的坐标是(3,3)
(3)当x>3时,y1>y2;当x<3时,y1<y2
(4)这两条直线与x轴所围成的三角形的面积为$\frac{27}{4}$
5.
(1)如图:

(2)交点A的坐标是(3,3)
(3)当x>3时,y1>y2;当x<3时,y1<y2
(4)这两条直线与x轴所围成的三角形的面积为$\frac{27}{4}$
查看更多完整答案,请扫码查看


