平面直角坐标系
概 念:如图,在平面内,两条互相
点的坐标:如图,对于平面内任意一点$P$,过点$P$分别向$x$轴、$y$轴作垂线,垂足在$x$轴、$y$轴上对应的数$a$,$b$分别称为点$P$的
象 限:如图,在平面直角坐标系中,两条坐标轴将坐标平面分成了四部分.右上方的部分称为第一象限,其他三部分按逆时针方向依次称为第二象限、第三象限和第四象限.坐标轴上的点不在任何一个象限内.
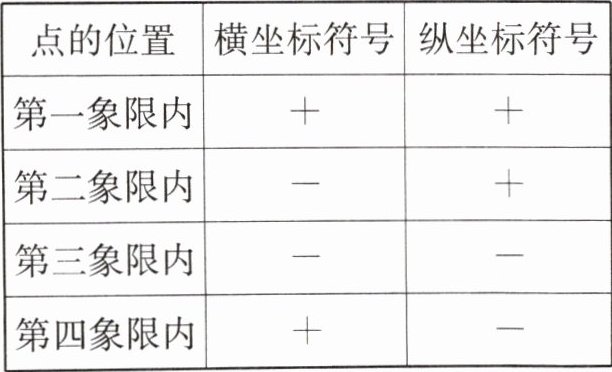
象限内点的坐标特征:
注 意:在平面直角坐标系中,对于平面上的任意一点,都有

概 念:如图,在平面内,两条互相
垂直
且有公共原点的数轴组成平面直角坐标系.通常,两条数轴分别置于水平位置与铅直位置,取向右与向上的方向分别为两条数轴的正方向.水平的数轴称为x
轴或横
轴,铅直的数轴称为y
轴或纵
轴,$x$轴和$y$轴统称坐标轴,它们的公共原点$O$称为平面直角坐标系的原点
.点的坐标:如图,对于平面内任意一点$P$,过点$P$分别向$x$轴、$y$轴作垂线,垂足在$x$轴、$y$轴上对应的数$a$,$b$分别称为点$P$的
横
坐标、纵
坐标,有序实数对$(a,b)$称为点$P$的坐标.象 限:如图,在平面直角坐标系中,两条坐标轴将坐标平面分成了四部分.右上方的部分称为第一象限,其他三部分按逆时针方向依次称为第二象限、第三象限和第四象限.坐标轴上的点不在任何一个象限内.
象限内点的坐标特征:
注 意:在平面直角坐标系中,对于平面上的任意一点,都有
唯一
的一个有序实数对(即点的坐标)与它对应;反过来,对于任意一个有序实数对,都有平面上唯一
的一点与它对应.

答案:
垂直 x 横 y 纵 原点 横 纵 唯一 唯一
1. 在平面直角坐标系中,点$A(2,-3)$位于(
A.第一象限
B.第二象限
C.第三象限
D.第四象限
D
)A.第一象限
B.第二象限
C.第三象限
D.第四象限
答案:
1.D
2. 如图,点$P$的横坐标是(

A.$1$
B.$2$
C.$(2,1)$
D.$(1,2)$
B
)
A.$1$
B.$2$
C.$(2,1)$
D.$(1,2)$
答案:
2.B
3. 已知点$A$在第二象限,请写一个符合要求的点$A$的坐标:
(-3,6)(答案不唯一)
.
答案:
3.(-3,6)(答案不唯一)
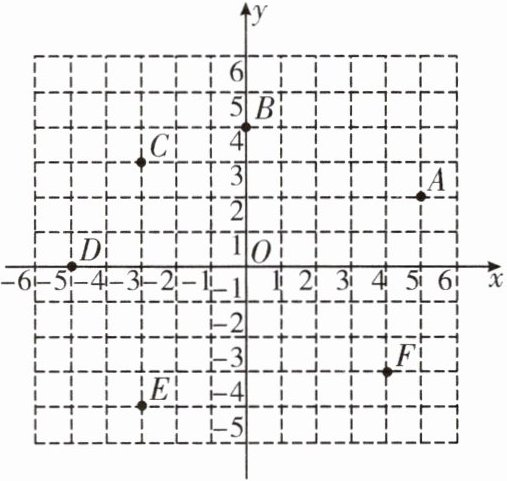
4. 如图,写出平面直角坐标系中点$A$,$B$,$C$,$D$,$E$,$F$的坐标.

答案:
4.点A,B,C,D,E,F的坐标分别为(5,2),(0,4),(-3,3),(-5,0),(-3,-4),(4,-3)
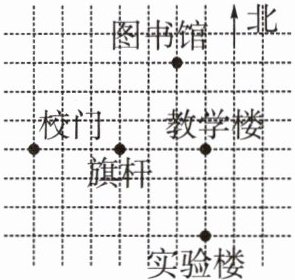
5. 如图,这是一所学校的平面示意图,建立适当的平面直角坐标系,并写出教学楼、校门和图书馆的坐标.

答案:
以旗杆所在位置为原点,水平向右为x轴正方向,竖直向上为y轴正方向,建立平面直角坐标系。
教学楼坐标:(3,0)
校门坐标:(-2,0)
图书馆坐标:(2,3)
教学楼坐标:(3,0)
校门坐标:(-2,0)
图书馆坐标:(2,3)
查看更多完整答案,请扫码查看


