21. (8 分) 如图, $OB, OD, OE$ 是 $\angle AOC$ 内部的三条射线, $OD$ 平分 $\angle AOB$, $\angle COE = 2\angle BOE$. 若 $\angle BOD = 25^{\circ}$, $\angle AOC = 140^{\circ}$, 求 $\angle COE$ 的度数.


答案:
解:因为OD平分$\angle AOB$,$\angle BOD=25^{\circ}$,所以$\angle AOB=2\angle BOD=50^{\circ}$.因为$\angle AOC=140^{\circ}$,所以$\angle BOC=140^{\circ}-\angle AOB=90^{\circ}$.因为$\angle COE=2\angle BOE$,$\angle COE+\angle BOE=\angle BOC$,所以$\angle BOE=30^{\circ}$,所以$\angle COE=2\angle BOE=60^{\circ}$.
22. (8 分)如图, 将两块直角三角尺的直角顶点 $C$ 叠放在一起.
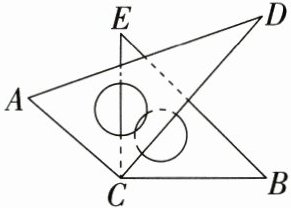
(1) 若 $\angle DCE = 40^{\circ}$, 求 $\angle ACB$ 的度数;
(2) 猜想 $\angle ACB$ 与 $\angle DCE$ 有怎样的数量关系? 并说明理由.

(1) 若 $\angle DCE = 40^{\circ}$, 求 $\angle ACB$ 的度数;
(2) 猜想 $\angle ACB$ 与 $\angle DCE$ 有怎样的数量关系? 并说明理由.
答案:
解:
(1)因为$\angle DCE=40^{\circ}$,$\angle ACD=90^{\circ}$,所以$\angle ACE=\angle ACD-\angle DCE=50^{\circ}$.因为$\angle BCE=90^{\circ}$,所以$\angle ACB=\angle ACE+\angle BCE=140^{\circ}$.
(2)$\angle ACB+\angle DCE=180^{\circ}$.理由:因为$\angle ACD=90^{\circ}$,所以$\angle ACE=90^{\circ}-\angle DCE$.又因为$\angle ACB=\angle ACE+90^{\circ}$,所以$\angle ACB=90^{\circ}-\angle DCE+90^{\circ}=180^{\circ}-\angle DCE$,即$\angle ACB+\angle DCE=180^{\circ}$.
(1)因为$\angle DCE=40^{\circ}$,$\angle ACD=90^{\circ}$,所以$\angle ACE=\angle ACD-\angle DCE=50^{\circ}$.因为$\angle BCE=90^{\circ}$,所以$\angle ACB=\angle ACE+\angle BCE=140^{\circ}$.
(2)$\angle ACB+\angle DCE=180^{\circ}$.理由:因为$\angle ACD=90^{\circ}$,所以$\angle ACE=90^{\circ}-\angle DCE$.又因为$\angle ACB=\angle ACE+90^{\circ}$,所以$\angle ACB=90^{\circ}-\angle DCE+90^{\circ}=180^{\circ}-\angle DCE$,即$\angle ACB+\angle DCE=180^{\circ}$.
查看更多完整答案,请扫码查看


