搜索
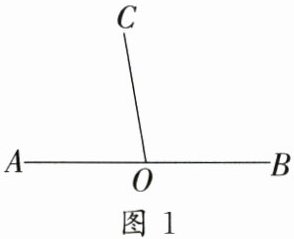
19. (13 分)已知点 $ O $ 为直线 $ AB $ 上一点,过点 $ O $ 作射线 $ OC $, $ \angle BOC = 100^{\circ} $.
(1)如图 1,求 $ \angle AOC $ 的度数；
(2)如图 2,过点 $ O $ 作射线 $ OD $,使 $ \angle COD = 90^{\circ} $,作 $ \angle AOC $ 的平分线 $ OM $,求 $ \angle MOD $ 的度数；
(3)如图 2,在(2)的条件下,作射线 $ OP $,若 $ \angle BOP $ 与 $ \angle AOM $ 互余,请画出图形,并求 $ \angle COP $ 的度数.
(1)如图 1,求 $ \angle AOC $ 的度数；
(2)如图 2,过点 $ O $ 作射线 $ OD $,使 $ \angle COD = 90^{\circ} $,作 $ \angle AOC $ 的平分线 $ OM $,求 $ \angle MOD $ 的度数；
(3)如图 2,在(2)的条件下,作射线 $ OP $,若 $ \angle BOP $ 与 $ \angle AOM $ 互余,请画出图形,并求 $ \angle COP $ 的度数.
答案：
解:
(1)$\angle AOC=180^{\circ}-\angle BOC=180^{\circ}-100^{\circ}=80^{\circ}$.
(2)由
(1),得$\angle AOC=80^{\circ}$.因为$\angle COD=90^{\circ}$,所以$\angle AOD=\angle COD-\angle AOC=10^{\circ}$.因为OM是$\angle AOC$的平分线,所以$\angle AOM=\frac{1}{2}\angle AOC=\frac{1}{2}× 80^{\circ}=40^{\circ}$,所以$\angle MOD=\angle AOM+\angle AOD=40^{\circ}+10^{\circ}=50^{\circ}$.
(3)由
(2),得$\angle AOM=40^{\circ}$.因为$\angle BOP$与$\angle AOM$互余,所以$\angle BOP+\angle AOM=90^{\circ}$,所以$\angle BOP=90^{\circ}-\angle AOM=90^{\circ}-40^{\circ}=50^{\circ}$.①当射线OP在$\angle BOC$内部时,如图,
$\angle COP=\angle BOC-\angle BOP=100^{\circ}-50^{\circ}=50^{\circ}$;②当射线OP在$\angle BOC$外部时,如图, 
$\angle COP=\angle BOC+\angle BOP=100^{\circ}+50^{\circ}=150^{\circ}$.综上所述,$\angle COP$的度数为$50^{\circ}$或$150^{\circ}$.
解:
(1)$\angle AOC=180^{\circ}-\angle BOC=180^{\circ}-100^{\circ}=80^{\circ}$.
(2)由
(1),得$\angle AOC=80^{\circ}$.因为$\angle COD=90^{\circ}$,所以$\angle AOD=\angle COD-\angle AOC=10^{\circ}$.因为OM是$\angle AOC$的平分线,所以$\angle AOM=\frac{1}{2}\angle AOC=\frac{1}{2}× 80^{\circ}=40^{\circ}$,所以$\angle MOD=\angle AOM+\angle AOD=40^{\circ}+10^{\circ}=50^{\circ}$.
(3)由
(2),得$\angle AOM=40^{\circ}$.因为$\angle BOP$与$\angle AOM$互余,所以$\angle BOP+\angle AOM=90^{\circ}$,所以$\angle BOP=90^{\circ}-\angle AOM=90^{\circ}-40^{\circ}=50^{\circ}$.①当射线OP在$\angle BOC$内部时,如图,
$\angle COP=\angle BOC-\angle BOP=100^{\circ}-50^{\circ}=50^{\circ}$;②当射线OP在$\angle BOC$外部时,如图, $\angle COP=\angle BOC+\angle BOP=100^{\circ}+50^{\circ}=150^{\circ}$.综上所述,$\angle COP$的度数为$50^{\circ}$或$150^{\circ}$. 20. (14 分)如图,线段 $ AB = 24 \space cm $,$ O $ 为线段 $ AB $ 上一点,且 $ AO : BO = 1 : 2 $,$ C $,$ E $ 顺次为射线 $ AB $ 上的动点,点 $ C $ 从 $ A $ 点出发向点 $ B $ 方向运动,$ E $ 点随之运动,且始终保持 $ CE = 8 \space cm $(动点 $ C $ 到达点 $ B $ 时停止运动),$ F $ 为 $ OE $ 的中点.
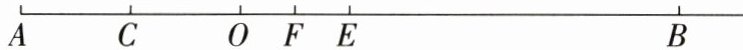
(1)当点 $ C $ 运动到 $ AO $ 的中点时,求 $ BF $ 的长；
(2)在点 $ C $ 的运动过程中,猜想线段 $ CF $ 和 $ BE $ 是否存在特定的数量关系,并说明理由.
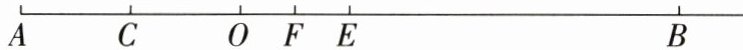
(1)当点 $ C $ 运动到 $ AO $ 的中点时,求 $ BF $ 的长；
(2)在点 $ C $ 的运动过程中,猜想线段 $ CF $ 和 $ BE $ 是否存在特定的数量关系,并说明理由.
答案：
解:因为$AB=24\ cm$,$AO:BO=1:2$,所以$AO=8\ cm$,$BO=16\ cm$.
(1)当点C运动到AO的中点时,$AC=OC=4\ cm$,又$CE=8\ cm$,所以$OE=4\ cm$,所以$BE=12\ cm$.又因为F为OE的中点,所以$FE=2\ cm$,所以$BF=14\ cm$.
(2)$2CF=BE$.理由略.
(1)当点C运动到AO的中点时,$AC=OC=4\ cm$,又$CE=8\ cm$,所以$OE=4\ cm$,所以$BE=12\ cm$.又因为F为OE的中点,所以$FE=2\ cm$,所以$BF=14\ cm$.
(2)$2CF=BE$.理由略.
查看更多完整答案，请扫码查看
