《2025年新坐标同步练习七年级数学上册人教版青海专用》

25. (12 分)点$A$,$B$,$C$在数轴上的位置如图所示。

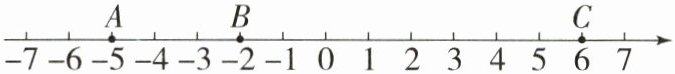
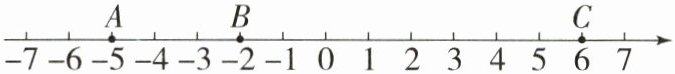
(1)点$B$表示的数是-2,点$C$表示的数是6。
(2)折叠数轴,使数轴上的点$B和点C$重合,则点$A$与表示数9的点重合。
(3)有理数$m$,$n在数轴上对应点之间的距离可表示为|m - n|$,如$5与2在数轴上所对应的点之间的距离为|5 - 2| = 3$。
①求$|x - 3| + |x - 6|$的最小值；
②若$M$,$N两点之间的距离为2 026$(点$M在点N$的左侧),将数轴折叠,使得$1对应的点与-3$对应的点重合,此时$M$,$N$两点也重合,求$M$,$N$两点分别表示的数。
(3)①当$|x-3|+|x-6|$的值最小时,x对应的点在3和6对应的点之间,所以当$3\leqslant x\leqslant 6$时,$|x-3|+|x-6|$的值最小,此时$|x-3|+|x-6|=x-3+6-x=3$.因此$|x-3|+|x-6|$的最小值是3.②因为1对应的点与-3对应的点重合,所以数轴在-1对应的点处折叠.因为M,N两点之间的距离为2026,所以点M,N与-1对应的点之间的距离均是1013,所以点M表示的数是$-1-1013=-1014$,点N表示的数是$-1+1013=1012$.

答案： 解:
(1)-2 6
(2)9
(3)①当$|x-3|+|x-6|$的值最小时,x对应的点在3和6对应的点之间,所以当$3\leqslant x\leqslant 6$时,$|x-3|+|x-6|$的值最小,此时$|x-3|+|x-6|=x-3+6-x=3$.因此$|x-3|+|x-6|$的最小值是3.②因为1对应的点与-3对应的点重合,所以数轴在-1对应的点处折叠.因为M,N两点之间的距离为2026,所以点M,N与-1对应的点之间的距离均是1013,所以点M表示的数是$-1-1013=-1014$,点N表示的数是$-1+1013=1012$.