19. (6 分)根据下列$a$的值,求代数式$\frac{a^2 - 3a + 1}{5}$的值:
(1)$a = 4$;
(2)$a = -\frac{1}{3}$.
(1)$a = 4$;
(2)$a = -\frac{1}{3}$.
答案:
解:
(1)当$a=4$时,原式$=\frac{16-12+1}{5}=1$.
(2)当$a=-\frac{1}{3}$时,原式$=\frac{\frac{1}{9}+1+1}{5}=\frac{19}{45}$.
(1)当$a=4$时,原式$=\frac{16-12+1}{5}=1$.
(2)当$a=-\frac{1}{3}$时,原式$=\frac{\frac{1}{9}+1+1}{5}=\frac{19}{45}$.
20. (10 分)已知$a$,$b$互为相反数,$c$,$d$互为倒数,$m的绝对值是2$,求代数式$\frac{|a + b|}{2m^2 + 1} + 4m - 3cd$的值.
答案:
解:由已知可得$a+b=0$,$cd=1$,$m=±2$.当$m=2$时,原式$=0+4×2-3=5$;当$m=-2$时,原式$=0+4×(-2)-3=-11$.综上所述,代数式$\frac{|a+b|}{2m^{2}+1}+4m-3cd$的值为5或$-11$.
21. (10 分)如图是一个长为$a$,宽为$b$的长方形,在它的四个角上各剪去一个边长为$x$的小正方形.
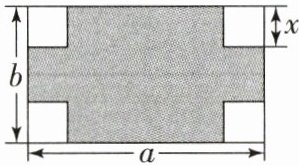
(1)用代数式表示图中阴影部分的面积;
(2)当$a = 8$,$b = 5$,$x = 2$时,求(1)中代数式的值.

(1)用代数式表示图中阴影部分的面积;
(2)当$a = 8$,$b = 5$,$x = 2$时,求(1)中代数式的值.
答案:
解:
(1)长方形的面积为$ab$,四个小正方形的面积和为$4x^{2}$,则阴影部分的面积为$ab-4x^{2}$.
(2)将$a=8$,$b=5$,$x=2$代入
(1)中代数式,得原式$=8×5-4×2^{2}=40-16=24$.
(1)长方形的面积为$ab$,四个小正方形的面积和为$4x^{2}$,则阴影部分的面积为$ab-4x^{2}$.
(2)将$a=8$,$b=5$,$x=2$代入
(1)中代数式,得原式$=8×5-4×2^{2}=40-16=24$.
查看更多完整答案,请扫码查看


