《2025年暑假作业甘肃教育出版社高一数学》

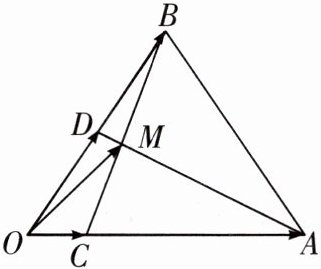
11. 如图所示,在$\triangle OAB$中,$\overrightarrow{OC}= \frac{1}{4}\overrightarrow{OA}$,$\overrightarrow{OD}= \frac{1}{2}\overrightarrow{OB}$,$AD与BC交于点M$,设$\overrightarrow{OA}= \boldsymbol{a}$,$\overrightarrow{OB}= \boldsymbol{b}$,试以$\boldsymbol{a},\boldsymbol{b}为基底表示\overrightarrow{OM}$。

答案： 解：设$\overrightarrow{OM}=m\boldsymbol{a}+n\boldsymbol{b}(m,n\in \mathbf{R})$，
则$\overrightarrow{AM}=\overrightarrow{OM}-\overrightarrow{OA}=(m - 1)\boldsymbol{a}+n\boldsymbol{b}$，
$\overrightarrow{AD}=\overrightarrow{OD}-\overrightarrow{OA}=\frac{1}{2}\boldsymbol{b}-\boldsymbol{a}=-\boldsymbol{a}+\frac{1}{2}\boldsymbol{b}$.
因为$A$，$M$，$D$三点共线，所以$\frac{m - 1}{-1}=\frac{n}{\frac{1}{2}}$，
即$m + 2n = 1$，
而$\overrightarrow{CM}=\overrightarrow{OM}-\overrightarrow{OC}=(m-\frac{1}{4})\boldsymbol{a}+n\boldsymbol{b}$，
$\overrightarrow{CB}=\overrightarrow{OB}-\overrightarrow{OC}=\boldsymbol{b}-\frac{1}{4}\boldsymbol{a}=-\frac{1}{4}\boldsymbol{a}+\boldsymbol{b}$，
因为$C$，$M$，$B$三点共线，所以$\frac{m-\frac{1}{4}}{-\frac{1}{4}}=\frac{n}{1}$，
即$4m + n = 1$.
由$\begin{cases}m + 2n = 1,\\4m + n = 1,\end{cases}$解得$\begin{cases}m=\frac{1}{7},\\n=\frac{3}{7},\end{cases}$
所以$\overrightarrow{OM}=\frac{1}{7}\boldsymbol{a}+\frac{3}{7}\boldsymbol{b}$.

12. 已知平行四边形的三个顶点的坐标分别是$(3,7)$,$(4,6)$,$(1,-2)$。求第四个顶点的坐标。

答案： 解：设平行四边形的三个顶点分别是$A(3,7)$，$B(4,6)$，$C(1,-2)$，第四个顶点为$D(x,y)$，
(1)当$\overrightarrow{AD}=\overrightarrow{BC}$时，$(x - 3,y - 7)=(-3,-8)$，
解得$x = 0$，$y = -1$，此时第四个顶点的坐标为$(0,-1)$；
(2)当$\overrightarrow{AD}=\overrightarrow{CB}$时，$(x - 3,y - 7)=(3,8)$，
解得$x = 6$，$y = 15$，此时第四个顶点的坐标为$(6,15)$；
(3)当$\overrightarrow{AB}=\overrightarrow{CD}$时，$(1,-1)=(x - 1,y + 2)$，
解得$x = 2$，$y = -3$，此时第四个项点的坐标为$(2,-3)$.
综上所述，第四个顶点的坐标为$(0,-1)$或$(6,15)$或$(2,-3)$.