《2025年启东中学作业本七年级数学上册苏科版徐州专版》

1. 若$∠1与∠2$互余,$∠3与∠2$互补,$∠4与∠3$是对顶角,则$∠4与∠1$的数量关系是(D)
A.$∠1= ∠4$
B.$∠4+∠1= 90^{\circ }$
C.$∠1-∠4= 90^{\circ }$
D.$∠4-∠1= 90^{\circ }$

答案： D

2. 如图,$∠AOB= ∠COD= ∠EOF= 90^{\circ }$,则$∠1$,$∠2$,$∠3$之间的数量关系为∠3−∠2+∠1=90°.

答案： ∠3−∠2+∠1=90°

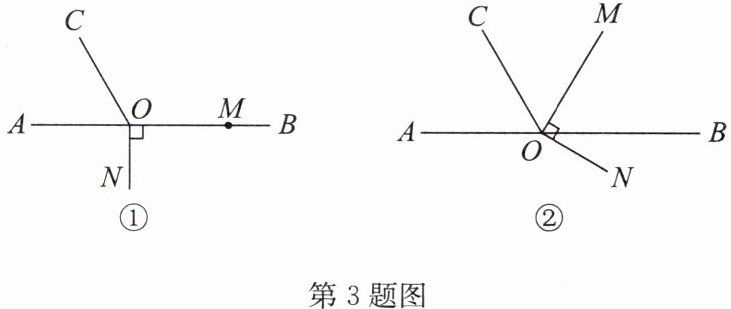
3. 如图①,$O为直线AB$上一点,过点$O作射线OC$,使$∠AOC:∠BOC= 1:2$,$∠MON的一边OM在射线OB$上,另一边$ON在直线AB$的下方,且$∠MON= 90^{\circ }$.
(1)如图①,$∠CON$的度数为____；
(2)如图②,将图①中的$∠MON绕点O以每秒20^{\circ }$的速度沿逆时针方向旋转一周,在旋转的过程中,若直线$ON恰好平分∠AOC$,求$∠MON运动的时间t$；
(3)在(2)的条件下,当$∠AOC与∠NOC$互余时,求出$∠BOC与∠MOC$之间的数量关系.

答案：

(1)150°
(2)解:当直线ON平分∠AOC时，分两种情况.
如答图①，当ON'平分∠AOC时，
因为∠AOC=60°，所以∠AON'=30°，
此时射线ON逆时针旋转60°，
所以∠MON运动的时间t=60°÷20°=3(秒);
如答图②，当ON平分∠AOC时，

因为ON平分∠AOC，
所以ON沿逆时针旋转的角度为90°+150°=240°，
所以∠MON运动的时间t=240°÷20°=12(秒).
综上所述，∠MON运动的时间t为3秒或12秒.
(3)解:如答图③所示，

因为∠AOC+∠NOC=90°，OM与OA重合，
所以∠BOC+∠MOC=180°.
如答图②，当ON平分∠AOC时，
∠AOC+∠NOC=90°，
所以∠NOC=30°，∠MOC=120°，∠BOC=120°，
所以∠BOC=∠MOC.
综上所述，∠BOC与∠MOC之间的数量关系为∠BOC+∠MOC=180°或∠BOC=∠MOC.