1. 关于 $x$ 的一元一次方程 $2x + m = 6$,其中 $m$ 是正整数. 若方程有正整数解,则 $m$ 的值为
2或4
.
答案:
2或4
2. 如图为一个计算程序. 若开始输入的 $x$ 为正整数,最后输出的结果为 $40$,则满足条件的 $x$ 的不同值有
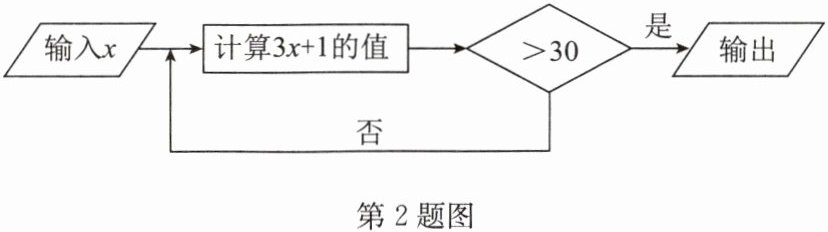
3
个.
答案:
3
3. 已知关于 $x$ 的方程 $9x - 3 = kx + 10$.
(1) 若这个方程的解是 $x = 2$,求 $k$ 的值;
(2) 当整数 $k$ 为何值时,方程有正整数解?并求出它的正整数解.
(1) 若这个方程的解是 $x = 2$,求 $k$ 的值;
(2) 当整数 $k$ 为何值时,方程有正整数解?并求出它的正整数解.
答案:
解:
(1)把x=2代入方程,得
18-3=2k+10,解得k=2.5.
(2)将方程移项、合并同类项,得(9-k)x=13,
解得x=$\frac{13}{9-k}$.
若方程有正整数解,则x=13或x=1.
当9-k=1,即k=8时,x=13;
当9-k=13,即k=-4时,x=1.
(1)把x=2代入方程,得
18-3=2k+10,解得k=2.5.
(2)将方程移项、合并同类项,得(9-k)x=13,
解得x=$\frac{13}{9-k}$.
若方程有正整数解,则x=13或x=1.
当9-k=1,即k=8时,x=13;
当9-k=13,即k=-4时,x=1.
查看更多完整答案,请扫码查看


